高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | |
| 1. 正接,正弦,余弦 | [無料] | |
| 2. 三角比の相互関係 | [無料] | |
| 3. 三角比の拡張 | [会員] | |
| 4. 正弦定理 | [会員] | |
| 5. 余弦定理 | [会員] | |
| 6. 三角形の面積 | [会員] |

1.正接・正弦・余弦
1.1 正接(tan)
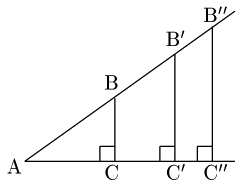
上の図において,△ABC∽△AB’C’∽△AB”C” であるから, \[\frac{{\rm BC}}{{\rm AC}}=\frac{{\rm B’C’}}{{\rm AC’}}=\frac{{\rm B^{\prime\prime}C^{\prime\prime}}}{{\rm AC^{\prime\prime}}}\] が成り立つ.この比(分数)の値は直角三角形の大きさにはよらず,$\angle{\rm A}$の大きさのみで決まる.
図の $\angle{\rm A}$ について,直角三角形の $\dfrac{\mbox{高さ}}{\mbox{底辺}}$ を $\angle{\rm A}$ の正接(せいせつ,タンジェント)という.
定義 正接(tan)
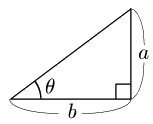
図において,$\dfrac ab$ を角θの正接 (tangent タンジェント)といい,$\tan\theta$ で表す: \[\tan\theta=\frac ab\]
覚え方
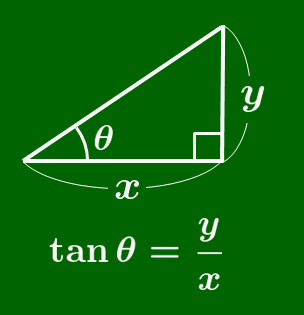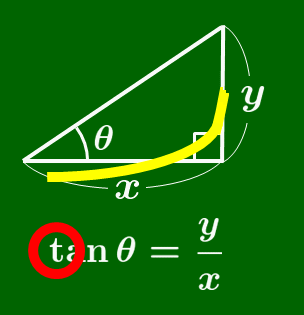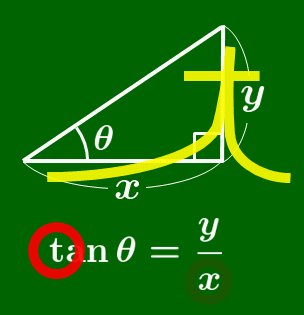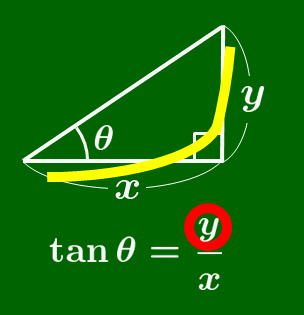
$\tan$ の覚え方
筆記体の $t$ を書く要領
例
次の3つの直角三角形は,3つの辺の比が簡単な値であることから特別な直角三角形として最もよく利用される.辺の比が図のようになることは三平方の定理(の逆)から確認できる.
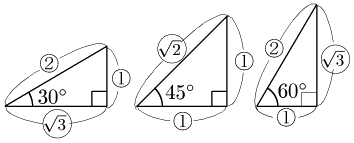
\[\begin{array}{lll} \tan30^\circ=\dfrac1{\sqrt3}, & \tan45^\circ=1, & \tan60^\circ=\sqrt3 \end{array}\]
補足1
$\tan$ の値は,例えば $\tan30^\circ=\dfrac1{\sqrt3}$ のように分母を有理化しないことも多い.この理由としては,$\dfrac{\sqrt3}3$ よりも表現がシンプルであることや,$\dfrac1{\sqrt3}$ の方が上の図のような直角三角形の辺の比をイメージしやすいことなどが考えられる.
補足2
次の2つの式は $\tan$ の分母を払っただけのものであるが,辺の長さを $\boldsymbol{\tan}$ で表現したものとして今後用いられる場面がある.
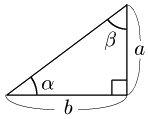
$\tan\alpha=\dfrac ab$ より,$a=b\tan\alpha$
$\tan\beta=\dfrac ba$ より,$b=a\tan\beta$

1.2 正弦(sin)・余弦(cos)

$\tan$ のときと同様に三角形の相似を考えると
\[\frac{{\rm BC}}{{\rm AB}}=\frac{{\rm B’C’}}{{\rm AB’}}=\frac{{\rm B^{\prime\prime}C^{\prime\prime}}}{{\rm AB^{\prime\prime}}}\]
\[\frac{{\rm AC}}{{\rm BA}}=\frac{{\rm AC’}}{{\rm B’A}}=\frac{{\rm AC^{\prime\prime}}}{{\rm B^{\prime\prime}A}}\]
といった比(分数)の値が,直角三角形の大きさによらず,$\angle{\rm A}$の大きさのみで決まる.
図の $\angle{\rm A}$ について,直角三角形の $\dfrac{\mbox{高さ}}{\mbox{斜辺}}$ を $\angle{\rm A}$ の正弦(せいげん,サイン)といい,$\dfrac{\mbox{底辺}}{\mbox{斜辺}}$ を $\angle{\rm A}$ の余弦(よげん,コサイン)という.
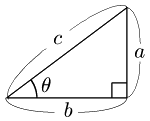
定義 正弦(sin)・余弦(cos)
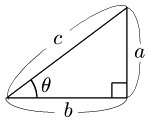
図において,
$\dfrac ac$ を,角θの正弦 (sine サイン)といい,$\sin\theta$ で表す.
$\dfrac bc$ を,角θの余弦 (cosine コサイン)といい,$\cos\theta$ で表す.
\[\begin{align*} &\sin\theta=\frac ac\\[5pt] &\cos\theta=\frac bc \end{align*}\]
覚え方
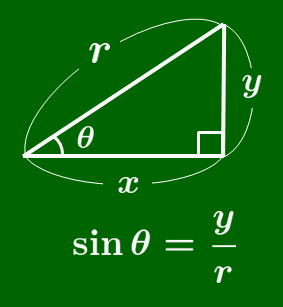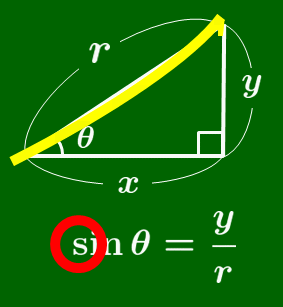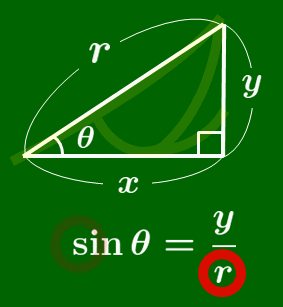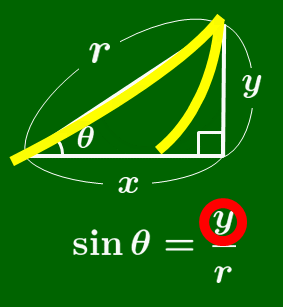
$\sin$ の覚え方
筆記体の $s$ を書く要領
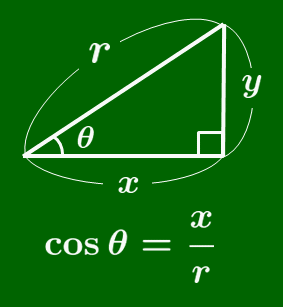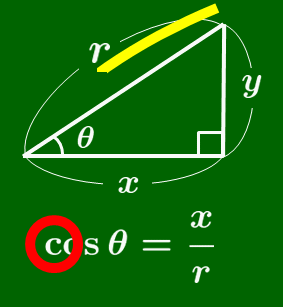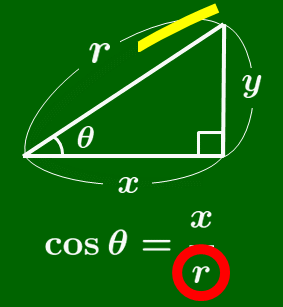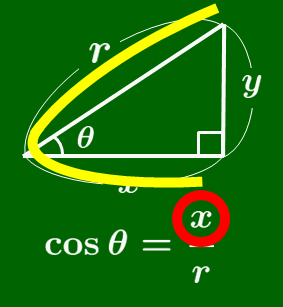
$\cos$ の覚え方
筆記体の $c$ を書く要領
例
$\sin,\ \cos$ も $\tan$ のときと同様に,次の特別な直角三角形における角が最もよく利用される.

\[\begin{array}{lll} \sin30^\circ=\dfrac12 & \sin45^\circ=\dfrac1{\sqrt2} & \sin60^\circ=\dfrac{\sqrt3}2\\[5pt] \cos30^\circ=\dfrac {\sqrt3}2 & \cos45^\circ=\dfrac1{\sqrt2} & \cos60^\circ=\dfrac12 \end{array}\]
補足
次の2つの式は $\tan$ のときと同様に分母を払っただけのものであるが,辺の長さを $\boldsymbol{\sin,\ \cos}$ で表現したものとして今後用いられる場面がそれなりにある.
$\sin\theta=\dfrac ac$ より,$a=c\sin\theta$
$\cos\theta=\dfrac bc$ より,$b=c\cos\theta$

次は,2.三角比の相互関係
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
演習問題
(1) ヒント1 ヒント2
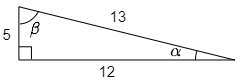
次の図の直角三角形について,
$\tan\alpha,\ \sin\alpha,\ \cos\alpha$,
$\tan\beta,\ \sin\beta,\ \cos\beta$
の各値を求めよ.
(2) ヒント
ある地点から高さ100mの塔の先端を見上げると,仰角が60°であった.その地点から塔の真下までの距離を求めよ.ただし,観測者の目の高さを1.5m,$\sqrt3=1.73$として計算し,小数第2位を四捨五入せよ.
(3) ヒント
傾き30°の上り坂を40m進むと,水平方向に何m進み,鉛直方向に何m上がったことになるか.ただし,$\sqrt3=1.73$として計算せよ.
(4) ヒント
半径 $r$ の円Oにおいて,弧ABに対する中心角∠AOBの大きさが $2\theta$ であるとき,弦ABの長さと,中心OからABに下ろした垂線OHの長さを,それぞれ $r$ と $\theta$ を用いて表せ.
(5) ヒント
半径10の円に内接する正方形の1辺の長さと,円の中心から1辺に下ろした垂線の長さをそれぞれ求めよ.
解答
角 $\alpha$ の三角比を考えるときは,角 $\alpha$ を左下に移動させて考えます. POINT
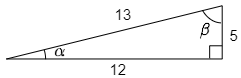
図より
\[\tan\alpha=\frac5{12},\ \sin\alpha=\frac5{13},\ \cos\alpha=\frac{12}{13}\]
同様にして,角 $\beta$ の三角比を考えるときは,角 $\beta$ を左下に移動させて考えます.