高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | [無料] | [会員] | |
| 2. 三角比の相互関係 | [無料] | [会員] | |
| 3. 三角比の拡張 | [会員] | ||
| 4. 正弦定理 | [会員] | [会員] | |
| 5. 余弦定理 | [会員] | [会員] | |
| 6. 三角形の面積 | [会員] | [会員] |

5.余弦定理
5.1 余弦定理
余弦定理とは
△ABCにおいて,3辺の長さと1つの角の大きさについて,次の余弦定理と呼ばれる関係が成り立つ:
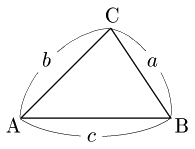
この定理により,三角形の3つの辺の長さと1つの角の大きさの合計4つの要素のうち,3つがわかっていれば,残り1つも求めることができる.ただし,わかっている3つの組合せによっては残り1つが1通りに定まらないこともある.その場合でも条件から更に吟味してどちらかに定められることもある.
証明の方針
$\boldsymbol{a^2=b^2+c^2-2bc\cos A}$ を示す場合
1.Cから直線ABに垂線CHを下ろす.
↓
2.△CBHで三平方の定理を利用.
証明
$a^2=b^2+c^2-2bc\cos A$ を示す.
1° $A$ が鋭角のとき
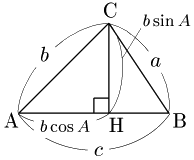
Cから辺ABまたはその延長上に垂線CHを引く.$B$ が鋭角,または鈍角のときは,△CBHにおいて三平方の定理により, \[{\rm CB}^2={\rm BH}^2+{\rm CH}^2\] \[\therefore a^2=|c-b\cos A|^2+(b\sin A)^2\] が成り立つ.$B$ が直角の場合は△CBHがつぶれてしまうが, $a=b\sin A$,$c=b\cos A$ であるから上の式はこの場合も含まれる.この式の右辺は \[\begin{align*} &(c^2-2bc\cos A+b^2\cos^2A)+b^2\sin^2A\\[5pt] =&b^2(\sin^2A+\cos^2A)+c^2-2bc\cos A\\[5pt] =&b^2+c^2-2bc\cos A \end{align*}\] となるから, \[a^2=b^2+c^2-2bc\cos A\] が成り立つ.
2° $A$ が直角のとき
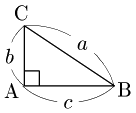
$\cos A=\cos90^\circ=0$ であるから, \[a^2=b^2+c^2-2bc\cos90^\circ\] すなわち \[a^2=b^2+c^2\] を示せばよいが,三平方の定理によりこれは成り立つ.
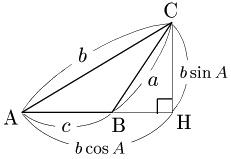
3° $A$ が鈍角のとき
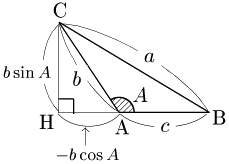
Cから辺ABの延長上に垂線CHを引く. \[\begin{align*} {\rm AH}&={\rm CA}\cos(180^\circ-A)\\[5pt] &=-{\rm CA}\cos A=-b\cos A\\[5pt] {\rm CH}&={\rm CA}\sin(180^\circ-A)\\[5pt] &=b\sin A \end{align*}\] 従って,△CBHにおいて三平方の定理により, \[{\rm CB}^2={\rm BH}^2+{\rm CH}^2\] \[\begin{align*} \therefore a^2&=\{c+(-b\cos A)\}^2+(b\sin A)^2\\[5pt] &=(c-b\cos A)^2+(b\sin A)^2 \end{align*}\] この式は,$A$ が鋭角のときと同じ式 であるから, \[a^2=b^2+c^2-2bc\cos A\] が成り立つ.
以上により,$a^2=b^2+c^2-2bc\cos A$ が示された.他の2式も同様に示される.
■
補足
2点間の距離という考え方なら場合分けは不要
上の証明では $A$ の大きさで3通りに場合分けして三平方の定理を利用したが,以下のように2点間の距離の公式 で導けば,場合分けは必要ない.数学Ⅱで学ぶ内容ではあるものの,三平方の定理から導けるもので,発展内容と呼ぶに値しない.
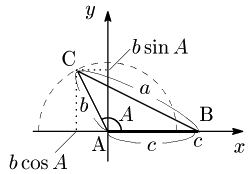
座標平面を用意し,△ABCを頂点Aが原点にくるようにして辺ABを $x$ 軸の正の部分に置き,頂点Cが $x$ 軸より上側の位置になるように配置する.
このとき,Bの座標は $(c,0)$ であり,また頂点Cの座標を $(x,y)$ とすると,原点を中心とする半径 $b$ の半円を考えて
\[\cos A=\frac xb,\ \ \sin A=\frac yb\]
\[\therefore x=b\cos A,\ \ y=b\sin A\]
となるから,頂点Cの座標は
\[(b\cos A,\ b\sin A)\]
である.よって,2点間の距離の公式により,
\[\begin{align*} {\rm BC}^2&=(c-b\cos A)^2+(0-b\sin A)^2\\[5pt] &=(c^2-2bc\cos A+b^2\cos^2A)+b^2\sin^2A\\[5pt] &=b^2(\sin^2A+\cos^2A)+c^2-2bc\cos A\\[5pt] &=b^2+c^2-2bc\cos A \end{align*}\]
■
例題 $b=2,\ c=3,\ A=60^\circ$ のとき,$a$ を求めよ.
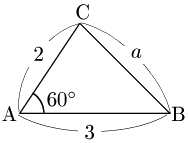
こたえ
解答例を表示する
5.2 余弦定理その2
上の余弦定理を変形しただけだが,利用頻度は高い
余弦定理 の3つの式を cos について解くと,次の式が得られる:
余弦定理その2 \[\begin{align*} \cos A&=\frac{b^2+c^2-a^2}{2bc}\\[5pt] \cos B&=\frac{c^2+a^2-b^2}{2ca}\\[5pt] \cos C&=\frac{a^2+b^2-c^2}{2ab} \end{align*}\]
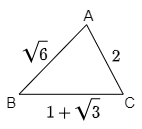
例題 △ABCにおいて,$a=1+\sqrt3$,$b=2$,$c=\sqrt6$ のとき,$B,\ C$ の大きさを求めよ.
こたえ
解答例を表示する補足
正弦定理も併用して考えることもできるが吟味が必要な場合も
$B=45^\circ$ が求まったあとでは,$C$ を正弦定理で求めることもできるが,$\sin$ では次のように吟味が必要になる場合がある:
正弦定理 により \[\frac2{\sin 45^\circ}=\frac{\sqrt6}{\sin C}\] \[\therefore \sin C=\frac{\sqrt6\sin45^\circ}2=\frac{\sqrt3}2\] $0^\circ< C< 135^\circ$ より,$C=60^\circ,\ 120^\circ$.(ここで吟味が必要.)
次の事実を使う:
三角形の辺と角の大小 三角形において,辺の長さの大小と,対応する角の大小は一致する.
(この定理の略証はスライド (会員向け)を参照.)
本問の場合,$a>c>b$ により $A>C>B$ となり,$C$ は最大の角ではないから鋭角.($C$ が $90^\circ$ 以上なら $A$ も $90^\circ$ 以上となり,そうすると三角形に $90^\circ$ 以上の角が2つもあることになってしまう!)
従って $\underline{\boldsymbol{C=60^\circ}}$

5.3 角の大小
鋭角,鈍角,直角の判定法
三角形の3辺の長さがわかっていれば,3つの角がそれぞれ鋭角なのか,鈍角なのか,直角なのかが判定できる.直角については中学で学んだ次の三平方の定理(の逆)から判定できる.

$\iff$ △ABCは辺BCを斜辺($\angle{\rm A}=90^\circ$)とする直角三角形
この結果から,$a^2\neq b^2+c^2$ のとき,$\angle{\rm A}\neq90^\circ$ であることがわかる.
それでは $a^2\neq b^2+c^2$ のとき,$\angle{\rm A} < 90^\circ$ なのだろうか?,それとも $\angle{\rm A} > 90^\circ$ だろうか?
余弦定理 $\cos A=\dfrac{b^2+c^2-a^2}{2bc}$ において,(分母)$ > 0$ であるから,
する.よって $0^\circ< A< 180^\circ$ のとき,
1° \[\begin{align*} A<90^\circ&\iff \cos A>0\\[5pt] &\iff b^2+c^2-a^2 > 0\\[5pt] &\iff a^2<b^2+c^2 \end{align*}\]
2° \[\begin{align*} A>90^\circ&\iff \cos A<0\\[5pt] &\iff b^2+c^2-a^2 < 0\\[5pt] &\iff a^2>b^2+c^2 \end{align*}\]
まとめ \[\begin{align*} a^2<b^2+c^2&\iff A < 90^\circ\\[5pt] a^2>b^2+c^2&\iff A > 90^\circ \end{align*}\]
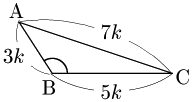
例題 △ABCにおいて,$\sin A:\sin B:\sin C=5:7:3$ のとき,△ABCは鋭角三角形,直角三角形,鈍角三角形のどれか.
こたえ
解答例を表示する
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | [無料] | [会員] | |
| 2. 三角比の相互関係 | [無料] | [会員] | |
| 3. 三角比の拡張 | [会員] | ||
| 4. 正弦定理 | [会員] | [会員] | |
| 5. 余弦定理 | [会員] | [会員] | |
| 6. 三角形の面積 | [会員] | [会員] |