2．三角比の相互関係(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅰ　第2章　三角比

	スライド	ノート
1. 正接，正弦，余弦	[無料]
2. 三角比の相互関係	[無料]
3. 三角比の拡張	[会員]
4. 正弦定理	[会員]
5. 余弦定理	[会員]
6. 三角形の面積	[会員]

2．三角比の相互関係

2.1　三角比の相互関係

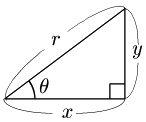
　上の図において三平方の定理により $x^2+y^2=r^2$ が成り立つ．$x=r\cos\theta,\ y=r\sin\theta$ であるから，これらを代入して，

\[ r^2\cos^2\theta+r^2\sin^2\theta=r^2\]

　両辺を $r^2$ で割って，

$\sin^2\theta+\cos^2\theta=1\ \ \cdots$ ①

　次に，

\[ \tan\theta=\frac yx=\frac{r\sin\theta}{r\cos\theta}=\frac{\sin\theta}{\cos\theta}\]

となるから，

$\tan\theta=\dfrac{\sin\theta}{\cos\theta}\ \ \cdots$ ②

　また，①の両辺を $\cos^2\theta$ で割ると，

\[ \frac{\sin^2\theta}{\cos^2\theta}+1=\frac 1{\cos^2\theta}\]

\[ \left(\frac{\sin\theta}{\cos\theta}\right)^2+1=\frac 1{\cos^2\theta}\]

　②を代入して

$1+\tan^2\theta=\dfrac1{\cos^2\theta}\ \ \cdots$ ③

　①～③は三角比における最重要公式としていつでも直ちに使えるよう記憶しておく必要がある．

三角比の相互関係
\[\begin{align*}
&[1]\ \sin^2\theta+\cos^2\theta=1\\[5pt]
&[2]\ \tan\theta=\frac{\sin\theta}{\cos\theta}\\[5pt]
&[3]\ 1+\tan^2\theta=\frac1{\cos^2\theta}
\end{align*}\]

例題1　$\theta$ は鋭角とする．$\cos\theta=\dfrac34$ のとき，$\sin\theta,\ \tan\theta$ の値を求めよ．

こたえ

　解答例を表示する >

　$\sin^2\theta+\cos^2\theta=1$ より，
\[ \sin^2\theta=1-\cos^2\theta=1-\left(\frac34\right)^2=\frac 7{16}\] 　$\sin\theta>0$ であるから，
\[ \sin\theta=\boldsymbol{\frac{\sqrt 7}4}\]
　また，
\[ \tan\theta=\frac{\sin\theta}{\cos\theta}=\frac{\frac{\sqrt7}4}{\frac34}=\boldsymbol{\frac{\sqrt7}3}\]

補足

　三平方の定理を用いて高さを計算し，図で考えるのもよい．

例題2　$\theta$ は鋭角とする．$\tan\theta=\dfrac34$ のとき，$\sin\theta,\ \cos\theta$ の値を求めよ．

こたえ

　解答例を表示する >

　$1+\tan^2\theta=\dfrac1{\cos^2\theta}$ より，
\[ \frac1{\cos^2\theta}=1+\left(\frac34\right)^2=\frac{25}{16}\]
\[\therefore \cos^2\theta=\frac{16}{25}\]
　$\cos\theta >0$ であるから，
\[\cos\theta=\boldsymbol{\frac45}\]
　また，$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ より，
\[\begin{align*} \sin\theta&=\tan\theta\cdot\cos\theta\\[5pt]
&=\frac 34\cdot\frac45=\boldsymbol{\frac35}
\end{align*}\]

2.2　$90^\circ-\theta$ の三角比

　$\theta$ が鋭角のとき，図より次が成り立つ：

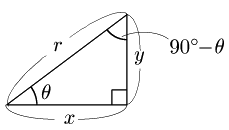
\[\begin{array}{ll}
\sin\theta=\dfrac yr,&\sin(90^\circ-\theta)=\dfrac xr\\[5pt]
\cos\theta=\dfrac xr,&\cos(90^\circ-\theta)=\dfrac yr\\[5pt]
\tan\theta=\dfrac yx,&\tan(90^\circ-\theta)=\dfrac xy
\end{array}\]

　よって，次のような関係が成り立つことがわかる：

90°-θ の三角比
\[\begin{align*}
&\sin(90^\circ-\theta)=\cos\theta\\[5pt]
&\cos(90^\circ-\theta)=\sin\theta\\[5pt]
&\tan(90^\circ-\theta)=\frac1{\tan\theta}
\end{align*}\]

次は，3．三角比の拡張
前は，1．正接，正弦，余弦

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

---

演習問題

解答

(1)　　ヒント
　次の三角比を $45^\circ$ 以下の三角比で表せ．
　　① $\sin65^\circ$　② $\cos82^\circ$　③ $\tan55^\circ$

　① $\sin65^\circ=\sin(90^\circ-25^\circ)=\cos25^\circ$
　② $\cos82^\circ=\cos(90^\circ-8^\circ)=\sin8^\circ$
　③ $\tan74^\circ=\tan(90^\circ-16^\circ)=\dfrac1{\tan16^\circ}$