このページにある内容は,こちらのスライド(会員向け)でわかり易く説明しています.
高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | |
| 1. 正接,正弦,余弦 | [無料] | |
| 2. 三角比の相互関係 | [無料] | |
| 3. 三角比の拡張 | [会員] | |
| 4. 正弦定理 | [会員] | |
| 5. 余弦定理 | [会員] | |
| 6. 三角形の面積 | [会員] |

6.三角形の面積
6.1 三角形の面積
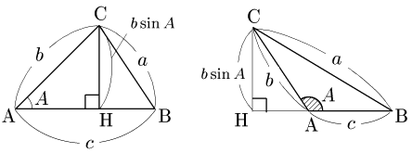
△ABCにおいて,Cから直線ABに垂線CHを引くと, \[{\rm CH}=b\sin A\] 故に, \[\triangle{\rm ABC}=\frac12\cdot{\rm AB}\cdot{\rm CH}=\frac12bc\sin A\]
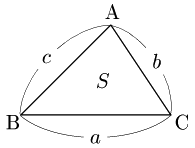
三角形の面積 △ABCの面積 $S$ は,
\[S=\frac12 bc\sin A=\frac12 ca\sin B=\frac12 ab\sin C\]
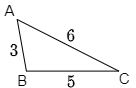
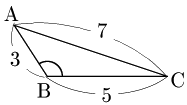
例題 △ABCにおいて,$a=5,\ b=7,\ c=3$ のとき,△ABCの面積 $S$ を求めよ.
こたえ

6.2 ヘロンの公式
ヘロンの公式 $s$ (小文字) を $s=\dfrac{a+b+c}2$ とすると,△ABC の面積 $S$ (大文字)は,
\[S=\sqrt{s(s-a)(s-b)(s-c)}\]

証明
余弦定理により,$\cos A=\dfrac{b^2+c^2-a^2}{2bc}$.
よって,
\[\begin{align*}
\sin^2A&=1-\cos^2A\\[5pt]
&=(1+\cos A)(1-\cos A)\\[5pt]
&=\left(1+\frac{b^2\!+\!c^2\!-\!a^2}{2bc}\right)\left(1-\frac{b^2\!+\!c^2\!-\!a^2}{2bc}\right)\\[5pt]
&=\frac{2bc\!+\!(b^2\!+\!c^2\!-\!a^2)}{2bc}\cdot\frac{2bc\!-\!(b^2\!+\!c^2\!-\!a^2)}{2bc}\\[5pt]
&=\frac{(b+c)^2-a^2}{2bc}\cdot\frac{a^2-(b-c)^2}{2bc}\\[5pt]
&=\frac{(b\!+\!c\!+\!a)(b\!+\!c\!-\!a)(a\!+\!b\!-\!c)(a\!-\!b\!+\!c)}{4b^2c^2}
\end{align*}\]
ここで,$a+b+c=2s$ とおくと,
\[\begin{align*}
(\mbox{分子})&=(a\!+\!b\!+\!c)(-a\!+\!b\!+\!c)(a\!-\!b\!+\!c)(a\!+\!b\!-\!c)\\[5pt]
&=2s\cdot2(s-a)\cdot2(s-b)\cdot2(s-c)\\[5pt]
&=16s(s-a)(s-b)(s-c)
\end{align*}\]
となるから,
\[\begin{align*}
\sin^2 A&=\frac{16s(s-a)(s-b)(s-c)}{4b^2c^2}\\[5pt]
&=\frac{4s(s-a)(s-b)(s-c)}{b^2c^2}
\end{align*}\]
$0^\circ < A < 180^\circ$ により,$\sin A > 0$ であるから,
\[\sin A=\frac{2\sqrt{s(s-a)(s-b)(s-c)}}{bc}\]
故に,
\[\begin{align*}
S&=\frac12bc\sin A\\[5pt]
&=\frac12bc\cdot\frac{2\sqrt{s(s-a)(s-b)(s-c)}}{bc}\\[5pt]
&=\sqrt{s(s-a)(s-b)(s-c)}
\end{align*}\]
■

6.3 三角比の応用
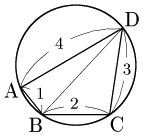
例題1 [円に内接する四角形の面積を求める]
AB=1,BC=2,CD=3,DA=4 である円に内接する四角形ABCDの面積 $S$ を求めよ.
こたえ

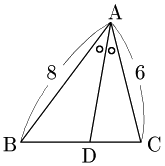
例題2 [角の二等分線の長さを求める]
AB=8, AC=6,$A=60^\circ$ の△ABC において,$\angle{\rm A}$ の二等分線と辺BCとの交点をDとする.線分ADの長さを求めよ.
こたえ

このページで疑問は解決されましたか?
こちらから数学に関するご質問・ご要望をお寄せください。
演習問題
解答
(1) ヒント
次のような平行四辺形ABCDの面積を求めよ.\[\rm AB=\sqrt2,\ BC=\sqrt6,\ \angle ABC=60^\circ\]
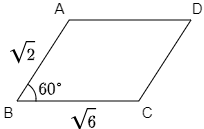
△ABCと△ACDは合同な三角形であるから
\[\begin{align*}
\mbox{求める面積}&=2\triangle{\rm ABC}\\[5pt]
&=2\left(\frac12{\rm AB\cdot BC} \sin60^\circ\right)\\[5pt]
&=2\left(\frac12\cdot \sqrt2\cdot\sqrt6\cdot\frac{\sqrt3}2\right)\\[5pt]
&=3
\end{align*}\]