このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

高校数学[総目次]

数学Ⅰ　第2章　三角比

  スライド ノート 問題
1. 正接，正弦，余弦 [会員]   [会員]
2. 三角比の相互関係 [会員]   [会員]
3. 三角比の拡張 [会員]    
4. 正弦定理 [会員]   [会員]
5. 余弦定理 [会員]   [会員]
6. 三角形の面積 [会員]   [会員]

4．正弦定理

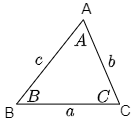
　このノートでは，△ABCにおいて下図のように，$\angle{\rm A}$，$\angle{\rm B}$，$\angle{\rm C}$ の大きさをそれぞれ $A,\ B,\ C$ (斜体)で表し，頂点A，B，Cの対辺BC，CA，ABをそれぞれ $a,b,c$ (小文字の斜体)で表すものとする．

4.1　辺の長さと正弦

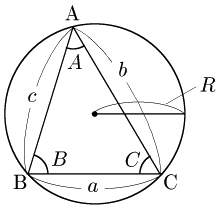
　正弦定理とは，三角形における辺の長さと対応する角の正弦(sin)に関する定理を指すが，その内容と証明を示す前に，正弦定理を導くための補助定理ともいうべき次の定理から確認していこう．といっても，この補助定理から正弦定理までは，目と鼻の先である．

(正弦定理を導くための)定理

　△ABCの外接円の半径を $R$ とすると，

\[\begin{align*} a&=2R\sin A,\\[5pt] b&=2R\sin B,\\[5pt] c&=2R\sin C \end{align*}\]

証明の流れ

  • 直径をとる
    　↓
  • 円周角の定理を用いて角を移動．
    　↓
  • 直角三角形で考える．

証明

1°　A < 90° のとき

アニメーション
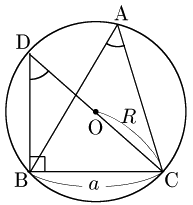
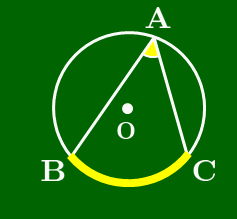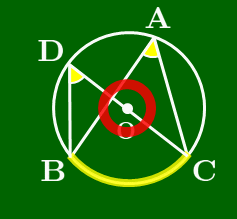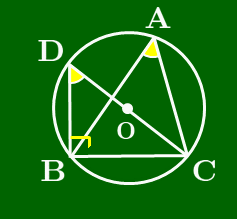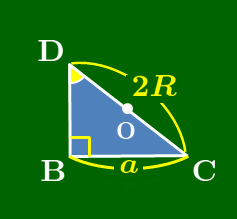
$\angle A$が鋭角のとき

証明の流れ①　直径CDをとる．

証明の流れ②　円周角の定理 により，

\[\angle{\rm A}=\angle{\rm D},\ \angle{\rm DBC}=90^\circ\]

証明の流れ③　直角三角形DBCにおいて，

\[{\rm BC}={\rm DC}\sin D\]

三角形の辺の長さを sin で表す方法についてはこちら を参照．

　DCは△BCDの外接円の直径であるから

\[a=2R\sin A\]

2°　A = 90° のとき

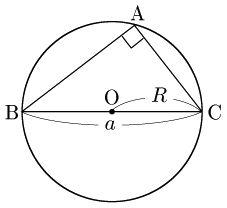
　${\rm BC}=2R,\ \sin A=\sin 90^\circ=1$ であるから，

\[a=2R\sin A\]

3°　A > 90° のとき

[ 上の1°(鋭角の場合)に帰着させて考える]

　Aを含まない方の弧BC上に，点Dを取る．
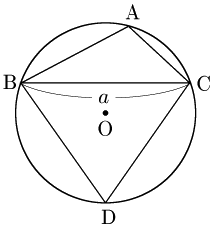
　四角形ABDCは円に内接するから，$A+D=180^\circ$．(数学A 図形の性質 5.円に内接する四角形 参照．)
　よって $D=180^\circ-A$．
　$A>90^\circ$ より $D<90^\circ$ であるから，1°により $a=2R\sin D$．
　ここで，$\sin D=\sin(180^\circ-A)=\sin A$ であるから，$a=2R\sin A$．

　以上により，$a=2R\sin A$ が示された．
　他の2つの式も同様に示される．

■

補足

　この定理から，三角形の3辺の長さの比が

\[\begin{align*} a:b:c&=2R\sin A:2R\sin B:2R\sin C\\[5pt] &=\sin A:\sin B:\sin C \end{align*}\]

となる．すなわち，三角形の辺の比は，対応する角の正弦の比に等しい．

重要な比例式 \[a:b:c=\sin A:\sin B:\sin C\]

間違えやすい注意

　$a:b:c=\angle {\rm A}:\angle {\rm B}:\angle {\rm C}$ ではない．

4.2　正弦定理

　上の定理で示された3つの式 から

\[\begin{align*} \frac a{\sin A}&=2R\\[5pt] \frac b{\sin B}&=2R\\[5pt] \frac c{\sin C}&=2R \end{align*}\]

と変形できるから，正弦定理と呼ばれる次の関係が成り立つ：

正弦定理 　△ABCの外接円の半径を $R$ とすると， \[\frac a{\sin A}=\frac b{\sin B}=\frac c{\sin C}=2R\]

　三角形の辺の長さや角度，また外接円の半径といった値を求める際に利用されるが，とりわけ「外接円の半径」という文言が問題文に現れたら，まずこの正弦定理の利用を疑ってかかるのが良かろう．

外接円の半径(キーワード)
→　正弦定理の利用

例題 　△ABCにおいて，$c=\sqrt6,\ A=75^\circ,\ C=60^\circ$ のとき，$b$ 及び外接円の半径 $R$ を求めよ．

こたえ

　解答例を表示する

次は　5．余弦定理
前は　3．三角比の拡張

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学Ⅰ　第2章　三角比

  スライド ノート 問題
1. 正接，正弦，余弦 [会員]   [会員]
2. 三角比の相互関係 [会員]   [会員]
3. 三角比の拡張 [会員]    
4. 正弦定理 [会員]   [会員]
5. 余弦定理 [会員]   [会員]
6. 三角形の面積 [会員]   [会員]