高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | |
| 1. チェバの定理 | [無料] | |
| 2. メネラウスの定理 | [無料] | |
| 3. チェバの定理の逆 | [無料] | |
| 4. メネラウスの定理の逆 | [会員] | |
| 5. 円に内接する四角形 | [会員] | |
| 6. 接弦定理とその逆 | [会員] | |
| 7. 方べきの定理とその逆 | [会員] | |
| 8. 三角形の五心 | ||
| 重心 | ||
| 外心 | ||
| 垂心 | ||
| 内心 | ||
| 傍心 |
中学校の範囲
| 1. 円周角の定理 | ||
| 2. 円周角の定理の逆 |

1.円に内接する四角形
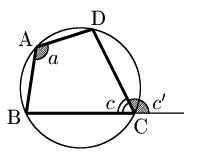
$\iff$ 対角の和が180° $(a\!+\!c\!=\!180^\circ)$
$\iff$ 内角が,その対角の外角に等しい ($a\!=\!c’$)
証明の方針
- 「四角形が円に内接する $\Rightarrow$ 対角の和が180°」は,円周角の定理を利用.
- 「四角形が円に内接する $\Leftarrow$ 対角の和が180°」は,△ABDの外接円上点${\rm C}\,’$ をとり,円周角の定理の逆を利用.
- 「対角の和が180°$\iff$内角が,その対角の外角に等しい」は明らか.
証明
「四角形が円に内接する $\Rightarrow$ 対角の和が180°」を示す.
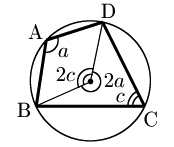
円周角の定理により図のようになるから,中心角に注目すると, \[2a+2c=360^\circ\] \[\therefore a+c=180^\circ\]
「四角形が円に内接する $\Leftarrow$ 対角の和が180°」を示す.
$\angle{\rm A}+\angle{\rm C}=180^\circ\ \cdots$① であるような四角形ABCDを考える:
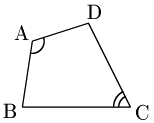
△ABDの外接円Oにおいて,下図のように弧BD上に点C $’$ をとる.
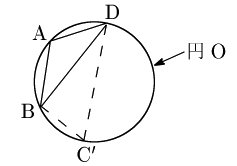
四角形AB${\rm C}\,’$Dは円に内接するから,先に示した事柄により,
\[\angle {\rm A}+\angle{\rm C}\,’=180^\circ\ \ \cdots\mbox{②}\]
である.
①,②より,$\angle{\rm C}=\angle{\rm C}\,’$.
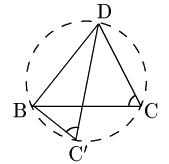
2点C,C$\,’$ が直線BDについて同じ側にあるから,円周角の定理の逆により4点B,$\rm{C}\,’$,C,Dは同一円周上,即ち円O上にある.
故に四角形ABCDは円Oに内接するから4点A,B,C,Dは同一円周上にある.
残るは「対角の和が180°$\iff$内角が,その対角の外角に等しい」の証明であるが,これは明らか.
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
演習問題
四角形が円に内接するということは,換言すれば4点が同一円周上にあるということです.4点が同一円周上にあるかどうか判定する問題に対処するためのトレーニングを中心にしていきましょう.
(1) 四角形ABCDはAD//BCの台形である.図のように2点A,Dを通る円と2辺AB,CDとの交点をそれぞれE,Fとすると,4点E,B,C,Fは同一円周上にあることを示せ.
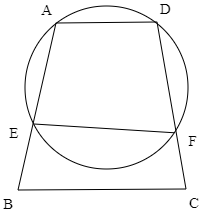
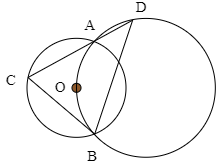
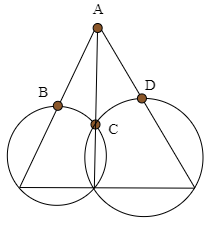
(2) 図のように円Oと,円Oの中心を通るもう一つの円があり,2点A,Bで交わっている.Aを通る直線が2点とC,Dで交わっているとき,BD=CDであることを示せ.
(3) 共通テスト対策!
図において,4点A,B,C,Dは同一円周上にあること示せ.

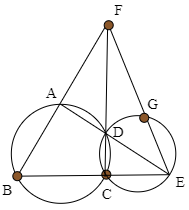
(4) 図のような円に内接する四角形ABCDにおいて,ADとBCの延長線の交点をE,ABとCDの延長線の交点をFとする.△CDEの外接円とEFの交点をGとするとき,4点F,B,C,Gは同一円周上にあることを示せ.

解答
(1) 四角形ABCDはAD//BCの台形である.図のように2点A,Dを通る円と2辺AB,CDとの交点をそれぞれE,Fとすると,4点E,B,C,Fは同一円周上にあることを示せ.

こたえ
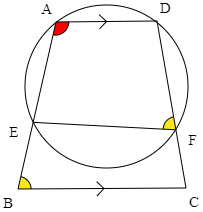
台形ABCDにおいて,AD//BCより