高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | |
| 1. チェバの定理 | [無料] | |
| 2. メネラウスの定理 | [無料] | |
| 3. チェバの定理の逆 | [無料] | |
| 4. メネラウスの定理の逆 | [会員] | |
| 5. 円に内接する四角形 | [会員] | |
| 6. 接弦定理とその逆 | [会員] | |
| 7. 方べきの定理とその逆 | [会員] | |
| 8. 三角形の五心 | ||
| 重心 | ||
| 外心 | ||
| 垂心 | ||
| 内心 | ||
| 傍心 |
中学校の範囲
| 1. 円周角の定理 | ||
| 2. 円周角の定理の逆 |

1.傍心
三角形の1つの内角の二等分線と,他の2つの角の外角の二等分線は1点で交わる.
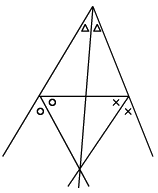

3本の角の二等分線が1点で交わる(傍心)
基本事項の確認
角の二等分線 $l$ は,2直線 $m, n$ から等しい距離にある点の集合である.
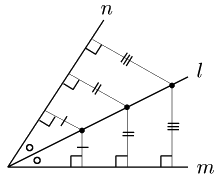
証明の方針
・2つの外角の二等分線の交点をとる.
↓
・その交点が,内角の二等分線上にあることを示す.
証明
△ABCにおいて,$\angle{\rm B}$の外角の二等分線と$\angle{\rm C}$の外角の二等分線との交点を${\rm I}_1$とし,${\rm I}_1$から直線BC,CA,ABに下ろした垂線の足をそれぞれD,E,Fとすると, \[{\rm I_1D}={\rm I_1E},\hspace{5mm} {\rm I_1D}={\rm I_1F}\] \[\therefore {\rm I_1E}={\rm I_1F}\]
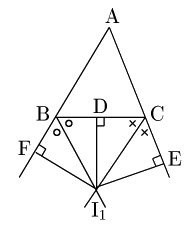
これは,${\rm I_1}$が$\angle{\rm A}$の二等分線上にあることを意味するから,三角形の1つの内角の二等分線と,他の2つの角の外角の二等分線は1点で交わる.
■
補足
すぐ上の図において,
\[\begin{gather} {\rm I_1D=I_1E=I_1F}\\[5pt] {\rm I_1D\perp BC,\ \ I_1E\perp CE,\ \ I_1F\perp BF} \end{gather}\]
であるから,1辺と他の2辺の延長線に接する円が存在する.
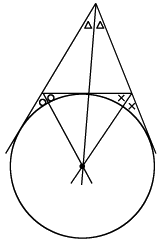
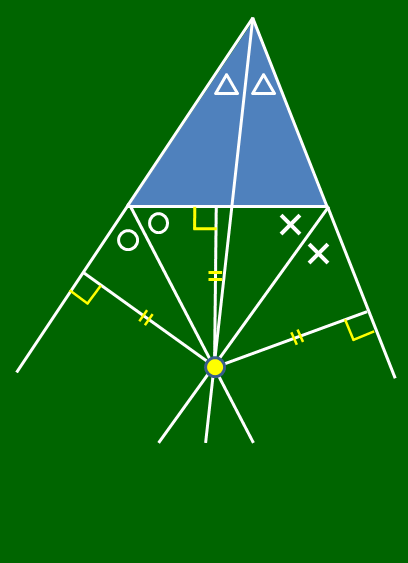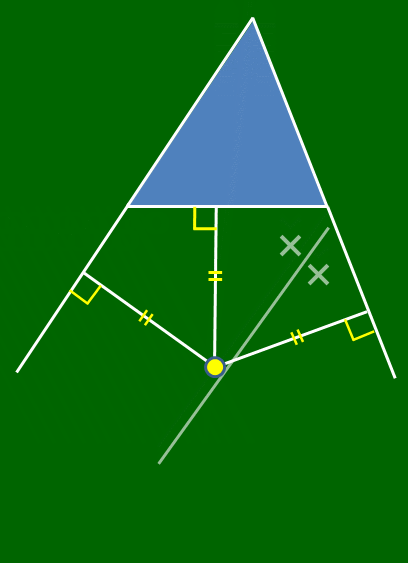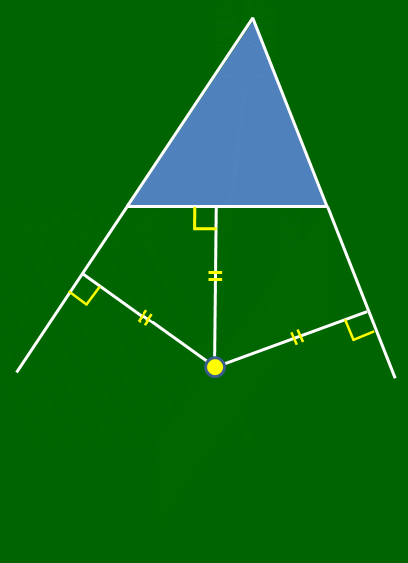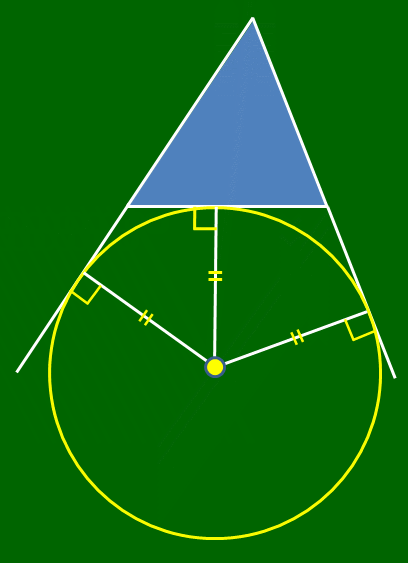
傍心を中心とし,図のように接する円(傍接円)が存在する.
この円を傍接円といい,傍接円の中心を傍心という.1つの三角形に対して,傍接円,傍心が3個ずつ存在する.
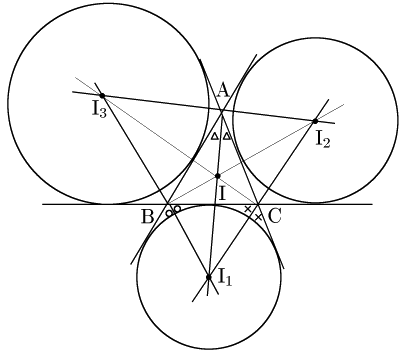
例題 △ABCの内心をI,3つの傍心を ${\rm I_1,\ I_2,\ I_3}$ とすると,Iは$\triangle{\rm I_1I_2I_3}$ の垂心であることを示せ.
こたえ
解答例を表示する >■

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | |
| 1. チェバの定理 | [無料] | |
| 2. メネラウスの定理 | [無料] | |
| 3. チェバの定理の逆 | [無料] | |
| 4. メネラウスの定理の逆 | [会員] | |
| 5. 円に内接する四角形 | [会員] | |
| 6. 接弦定理とその逆 | [会員] | |
| 7. 方べきの定理とその逆 | [会員] | |
| 8. 三角形の五心 | ||
| 重心 | ||
| 外心 | ||
| 垂心 | ||
| 内心 | ||
| 傍心 |
中学校の範囲
| 1. 円周角の定理 | ||
| 2. 円周角の定理の逆 |