6．接弦定理とその逆(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学A　第3章　図形の性質

第3章　図形の性質

	スライド	ノート	問題
1. チェバの定理	[無料]		[会員]
2. メネラウスの定理	[無料]		[会員]
3. チェバの定理の逆	[無料]
4. メネラウスの定理の逆	[会員]
5. 円に内接する四角形	[会員]		[会員]
6. 接弦定理とその逆	[会員]
7. 方べきの定理とその逆	[会員]
8. 三角形の五心
重心
外心
垂心
内心
傍心

---

中学校の範囲

	スライド	ノート	問題
1. 円周角の定理			[会員]
2. 円周角の定理の逆			[会員]

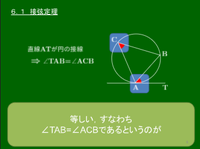
1．接弦定理

証明

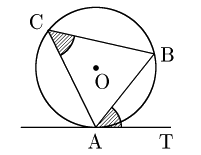
[1] ∠TABが鋭角のとき

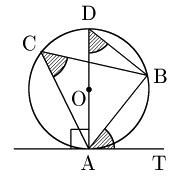
　直径AODをとると，∠ACB$=$∠ADB（∵円周角の定理）より，

$$\angle{\rm TAB}=\angle{\rm ADB}\ \ \cdots(*)$$

を示せばよい．

$$\begin{align*} \angle{\rm TAB}&=\angle{\rm DAT}-\angle{\rm DAB}\\[5pt] &=\ 90^\circ-\angle{\rm DAB}\ \ \cdots\mbox{①} \end{align*}$$

　また，半円の弧に対する円周角は90°であるから∠ABD$=$90°．よって△ABDの内角の関係より，

$$\begin{align*} \angle{\rm ADB}&=180^\circ-(\angle{\rm ABD}+\angle{\rm DAB})\\[5pt] &=180^\circ-(\ 90^\circ+\angle{\rm DAB})\\[5pt] &=\ 90^\circ-\angle{\rm DAB}\ \ \cdots\mbox{②} \end{align*}$$

　よって，①，②より $(*)$ が示された．

[2] ∠TABが直角のとき

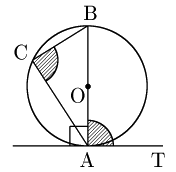
　半円の弧に対する円周角は90°であるから∠TAB$=$∠ACBは成り立つ．

[3] ∠TABが鈍角のとき

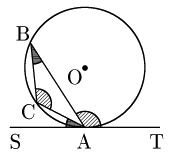
　図のように点Sをとると，∠SACは鋭角であるから，先に示した[1]により

$$\angle{\rm SAC}=\angle{\rm ABC}$$

　よって，∠SAT$=$180°であるから，

$$\begin{align*} \angle{\rm TAB}&=180^\circ-(\angle{\rm SAC}+\angle{\rm CAB})\\[5pt] &=180^\circ-(\angle{\rm ABC}+\angle{\rm CAB})\ \ \cdots\mbox{③} \end{align*}$$

　一方，△ABCの内角の関係より

$$\angle{\rm ACB}=180^\circ-(\angle{\rm ABC}+\angle{\rm CAB})\ \ \cdots\mbox{④}$$

　③，④より∠TAB$=$∠ACBが示された．

■

2．接弦定理の逆

証明の流れ

1．点Aを通る接線上に点T$’$をとる．
　　↓
2. 上で示した接弦定理を利用

証明

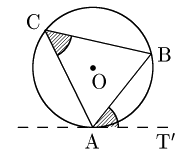
　図のように点Aを通る円の接線上に点T$’$をとると，接弦定理により

$$\angle{\rm T’AB}=\angle{\rm ACB}$$

が成り立つ．よって仮定の式とから，

$$\angle{\rm TAB}=\angle{\rm T’AB}$$

　従って2直線AT，AT’は一致するから，直線ATは円の接線である．

■

---

高校数学[総目次]

数学A　第3章　図形の性質

第3章　図形の性質

	スライド	ノート	問題
1. チェバの定理	[無料]		[会員]
2. メネラウスの定理	[無料]		[会員]
3. チェバの定理の逆	[無料]
4. メネラウスの定理の逆	[会員]
5. 円に内接する四角形	[会員]		[会員]
6. 接弦定理とその逆	[会員]
7. 方べきの定理とその逆	[会員]
8. 三角形の五心
重心
外心
垂心
内心
傍心

---

中学校の範囲

	スライド	ノート	問題
1. 円周角の定理			[会員]
2. 円周角の定理の逆			[会員]