高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | |
| 1. チェバの定理 | [無料] | |
| 2. メネラウスの定理 | [無料] | |
| 3. チェバの定理の逆 | [無料] | |
| 4. メネラウスの定理の逆 | [会員] | |
| 5. 円に内接する四角形 | [会員] | |
| 6. 接弦定理とその逆 | [会員] | |
| 7. 方べきの定理とその逆 | [会員] | |
| 8. 三角形の五心 | ||
| 重心 | ||
| 外心 | ||
| 垂心 | ||
| 内心 | ||
| 傍心 |
中学校の範囲
| 1. 円周角の定理 | ||
| 2. 円周角の定理の逆 |

1.チェバの定理
直線AB,BC,CA上にない点Oをとる.△ABCの頂点A,B,Cと点Oを結ぶ各直線が対辺,またはその延長とそれぞれP,Q,Rで交わるとき,次が成り立つ:
\[\boldsymbol{\frac{\rm BP}{\rm PC}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}=1}\]
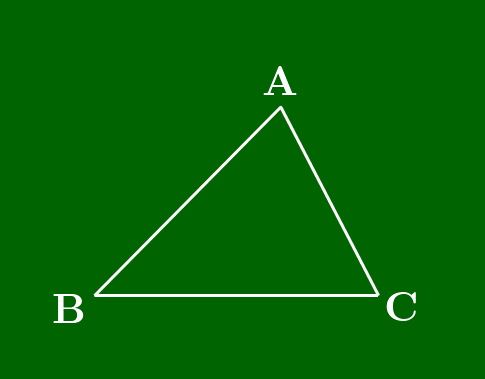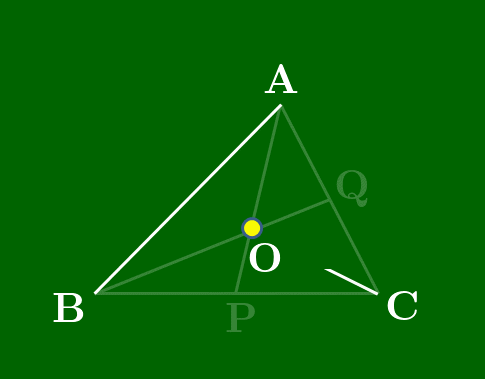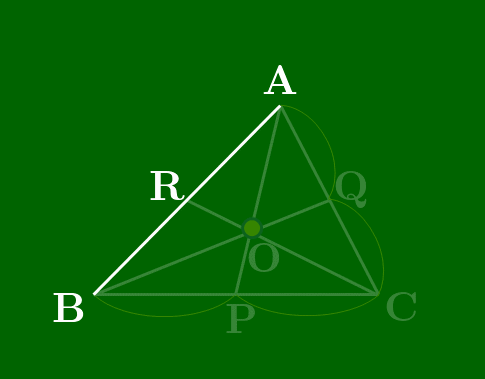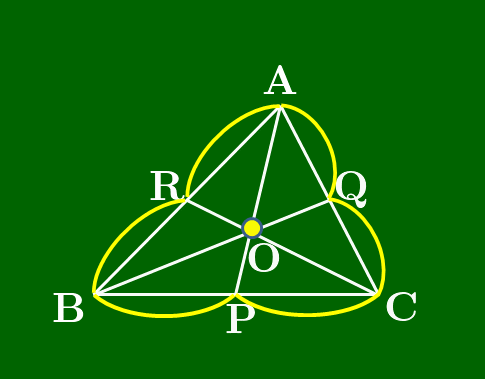
(スライドから抜粋)
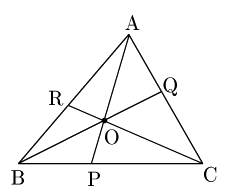
点が△ABCの内部にある場合
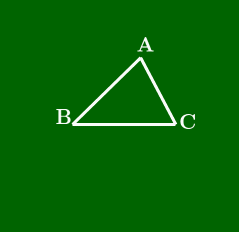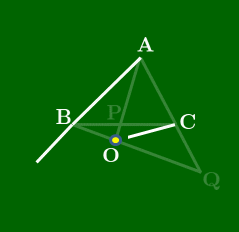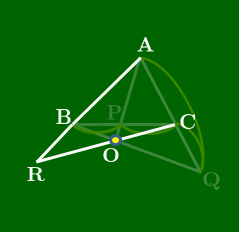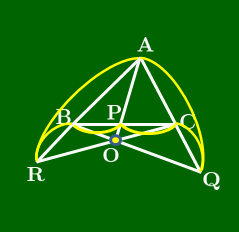
(スライドから抜粋)
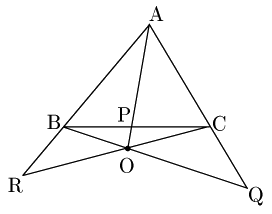
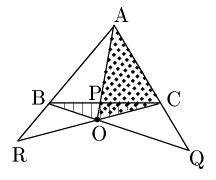
点が△ABCの外部にある場合
証明のポイント
3つの線分比の値(分数)を,三角形の面積比の値で表す.
確認事項
- 比 $a:b$ について,$\dfrac ab$ を比の値という.$\dfrac ab=\dfrac cd$ が成り立つとき,$a:b=c:d$ と表す.
証明
1° 点Oが△ABCの内部にあるとき
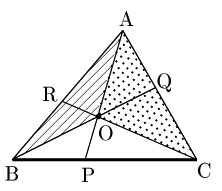
\[\rm BP:PC=\triangle OAB:\triangle OCA\]
\[ \therefore \frac{\rm BP}{\rm PC}=\frac{\triangle \rm OAB}{\triangle \rm OCA}\ \ \cdots\ \mbox{①}\]
同様にして,
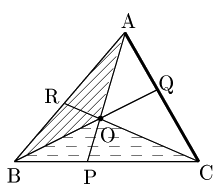
\[\frac{\rm CQ}{\rm QA}=\frac{\triangle \rm OCB}{\triangle \rm OAB}\ \ \cdots\ \mbox{②}\]
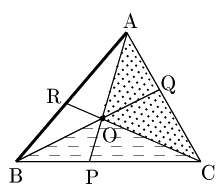
\[\frac{\rm AR}{\rm RB}=\frac{\triangle \rm OCA}{\triangle \rm OCB}\ \ \cdots\ \mbox{③}
\]
①,②,③を辺々掛けて
\[\begin{align*}
&\frac{\rm BP}{\rm PC}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}\\[5pt]
=&\ \frac{\triangle \rm OAB}{\triangle \rm OCA}\cdot\frac{\triangle \rm OCB}{\triangle \rm OAB}\cdot\frac{\triangle \rm OCA}{\triangle \rm OCB}\\[5pt]
=&\ 1
\end{align*}\]
2° 点Oが△ABCの外部にあるとき
点Oが△ABCの内部にある場合とは図が異なるだけで,式は異なるところが1つもない.
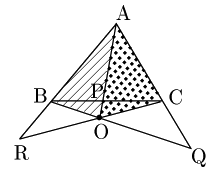
\[\rm BP:PC=\triangle OAB:\triangle OCA\]
\[ \therefore \frac{\rm BP}{\rm PC}=\frac{\triangle \rm OAB}{\triangle \rm OCA}\ \ \cdots\ \mbox{④}\]
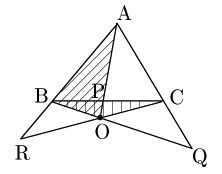
\[\frac{\rm CQ}{\rm QA}=\frac{\triangle \rm OCB}{\triangle \rm OAB}\ \ \cdots\ \mbox{⑤}\]
\[\frac{\rm AR}{\rm RB}=\frac{\triangle \rm OCA}{\triangle \rm OCB}\ \ \cdots\ \mbox{⑥}
\]
④,⑤,⑥を辺々掛けて
\[\begin{align*}
&\frac{\rm BP}{\rm PC}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}\\[5pt]
=&\ \frac{\triangle \rm OAB}{\triangle \rm OCA}\cdot\frac{\triangle \rm OCB}{\triangle \rm OAB}\cdot\frac{\triangle \rm OCA}{\triangle \rm OCB}\\[5pt]
=&\ 1
\end{align*}\]
補足
- 分子→分母→分子→分母→ … という順でアルファベットがしりとり式に続いていく.
- 加えて,頂点→分点→頂点→分点→… の順でアルファベットを書く.
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
演習問題
(1) [難易度 易]
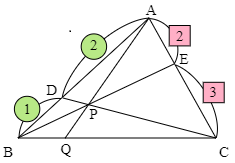
△ABCにおいて,辺ABを $2:1$ に内分する点をD,辺ACを $2:3$ に内分する点をEとし,BE,CDの交点をPとする.直線APと辺BCとの交点をQとするとき,$\rm{BQ:QC}$ を求めよ.
(2) [難易度 標準]
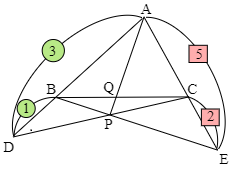
△ABCにおいて,辺ABを $3:1$ に外分する点をD,辺ACを $5:2$ に外分する点をEとし,BE,CDの交点をPとする.直線APとBCとの交点をQとするとき,$\rm{BQ:QC}$ を求めよ.
(3) [難易度 標準]
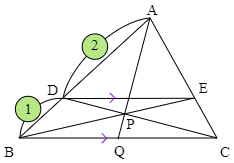
△ABCにおいて,辺AB上を $2:1$ に内分する点をDとし,Dを通ってBCに平行な直線とACとの交点をEとする.BE,CDの交点をPとし,直線APとBCとの交点をQとするとき,QはBCの中点であることを示せ.
解答
チェバの定理の式は辺の長さを用いた式になっていますが,例えば $\rm{\dfrac{BQ}{QC}}$ という部分は $\rm{BQ:QC}$ の比の値です.従って辺の長さそのものがわからなくても,比の値さえわかればよいという訳です. POINT