4．メネラウスの定理の逆(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学A　第3章　図形の性質

第3章　図形の性質

	スライド	ノート	問題
1. チェバの定理	[無料]		[会員]
2. メネラウスの定理	[無料]		[会員]
3. チェバの定理の逆	[無料]
4. メネラウスの定理の逆	[会員]
5. 円に内接する四角形	[会員]		[会員]
6. 接弦定理とその逆	[会員]
7. 方べきの定理とその逆	[会員]
8. 三角形の五心
重心
外心
垂心
内心
傍心

---

中学校の範囲

	スライド	ノート	問題
1. 円周角の定理			[会員]
2. 円周角の定理の逆			[会員]

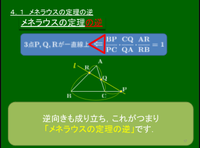
1．メネラウスの定理の逆

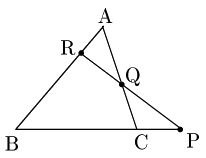
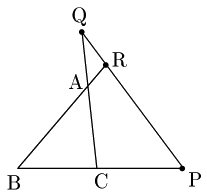
証明の流れ

[1]　直線QRと直線BCとの交点P$’$ をとる．
　　　[3点P$’$ ，Q，Rは一直線上]
　　　　↓
[2]　△ABCと直線P$’$Q でメネラウスの定理の式を作る．
　　　　↓
[3]　[2] の式と与えられた式を比較
　　　　↓
[5]　PとP$’$ が一致
つまり，[1]よりP，Q，Rは一直線上にある．

証明

1°　1点Pのみが辺の延長上にあるとき

　直線QR，BCとの交点をP$’$とする．(←流れの[1])
　[3点P$’$ ，Q，Rは一直線上]

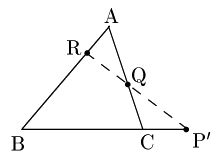
　△ABCと直線P$’$Q でメネラウスの定理 により $$\frac{\rm BP’}{\rm P’C}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}=1$$ が成り立つ．(←流れの[2])

　これと，与えられた式 $$\frac{\rm BP}{\rm PC}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}=1$$ を比較すると， $$\frac{\rm BP’}{\rm P’C}=\frac{\rm BP}{\rm PC}$$ が成り立つから， $$\rm BP’:P’C=BP:PC$$ である．(←流れの[3])

　よって，2点P$’$，Pは共に，線分BCを同じ比で外分する点であるから一致する．P$’$ は直線QR上に取ったのであるから，3点P，Q，Rは1直線上にある．(←流れの[4])

2°　3点P,Q,Rが円の延長上にあるとき

　※ 1°との違いは図のみ．記述部分は一字一句同じ．

　直線QR，BCとの交点をP$’$とする．(←流れの[1])
　[3点P$’$ ，Q，Rは一直線上]

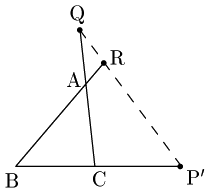
　△ABCと直線P$’$Q でメネラウスの定理 により $$\frac{\rm BP’}{\rm P’C}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}=1$$ が成り立つ．(←流れの[2])

　これと，与えられた式 $$\frac{\rm BP}{\rm PC}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}=1$$ を比較すると， $$\frac{\rm BP’}{\rm P’C}=\frac{\rm BP}{\rm PC}$$ が成り立つから， $$\rm BP’:P’C=BP:PC$$ である．(←流れの[3])

　よって，2点P$’$，Pは共に，線分BCを同じ比で外分する点であるから一致する．P$’$ は直線QR上に取ったのであるから，3点P，Q，Rは1直線上にある．(←流れの[4])

■

補足

「チェバの定理の逆」との主な違いは次の赤線部分である：

---

高校数学[総目次]

数学A　第3章　図形の性質

第3章　図形の性質

	スライド	ノート	問題
1. チェバの定理	[無料]		[会員]
2. メネラウスの定理	[無料]		[会員]
3. チェバの定理の逆	[無料]
4. メネラウスの定理の逆	[会員]
5. 円に内接する四角形	[会員]		[会員]
6. 接弦定理とその逆	[会員]
7. 方べきの定理とその逆	[会員]
8. 三角形の五心
重心
外心
垂心
内心
傍心

---

中学校の範囲

	スライド	ノート	問題
1. 円周角の定理			[会員]
2. 円周角の定理の逆			[会員]