高校数学[総目次]
数学Ⅱ 第3章 図形と方程式
| スライド | ノート | 問題 | |
| 1. 座標平面上の点 | |||
| 2. 直線の方程式 | |||
| 3. 円の方程式 | |||
| 4. 円と直線 | |||
| 5. 軌跡と方程式 | |||
| 6. 不等式と領域 |

4.円と直線
4.1 円と直線の位置関係
円と直線の位置関係には2つのアプローチの方法がある
円と直線の位置関係には次の3通りがある.
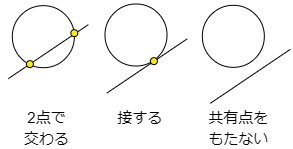
これらを次の2通りによって特徴付けする.
[1] 判別式
[2] 中心と直線の距離
例題 円C $:(x\!-\!3)^2\!+\!(y\!-\!2)^2\!=\!1$ と,直線 $l:x\!-\!2y\!+\!3\!=\!0$ の共有点の個数を求めよ.
[1] 判別式からのアプローチ
$l$ の式より,$y=\dfrac12x+\dfrac32$
$C$ の式に代入して, \[(x-3)^2+\left\{\left(\frac12 x+\frac32\right)-2\right\}^2=1\]
整理して \[5x^2-26x+33=0\]
この2次方程式の解がもし実数なら,それは円と直線の共有点の $x$ 座標を表す.つまり
共有点の個数と実数解の個数は一致する.
この2次方程式を実際に解けばどのような解をもつかはもちろんわかるが,実数解の個数を調べるだけならそこまでしなくとも判別式で十分である.判別式を $D$ とすると
\[\begin{align*}
D/4&=(-13)^2-5\times33\\[5pt]
&=169-165\\[5pt]
&=4>0
\end{align*}\]
よって,円と直線は異なる2点で交わる.
一般に,
円 :$(x-a)^2+(y-b)^2=r^2$
直線:$y=mx+n$
の2式から $y$ を消去して得られる $x$ の2次方程式が実数解をもてば,それは円と直線の共有点の $x$ 座標を表すから,次が成り立つ:
円と直線の位置関係[1] 円 $(x\!-\!a)^2\!+\!(y\!-\!b)^2\!=\!r^2$ と直線 $y\!=\!mx\!+\!n$ から $y$ を消去して得られる2次方程式の判別式を$D$とすると,\begin{align*}
&D>0\iff\mbox{異なる2点で交わる}\\
&D=0\iff\mbox{接する}\\
&D<0\iff\mbox{共有点をもたない}
\end{align*}
[2] 中心と直線の距離からのアプローチ
円の中心 $(3,2)$ と直線 $x-2y+3=0$ の距離は,
\[\frac{|3-2\times2+3|}{\sqrt{1^2+(-2)^2}}=\frac2{\sqrt 5}(= 0.89\cdots)\]
この値は円の半径である1より小さい.
よって,円と直線は異なる2点で交わる.
一般に,円の半径を $r$,中心と直線の距離を $d$ とする.$r$ と $d$ の大小関係により次が成り立つ:
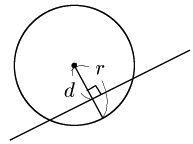
円と直線の位置関係[2] 半径 $r$ の円の中心と直線の距離を $d$ とすると,\begin{align*}
&d<r\iff\mbox{異なる2点で交わる}\\
&d=r\iff\mbox{接する}\\
&d>r\iff\mbox{共有点をもたない}
\end{align*}
補足
この例からわかるように,円と直線の位置関係の問題では,「中心と直線の距離からのアプローチ」の方が,一般には計算が平易.

4.2 円の接線の方程式
円周上の点における接線の方程式は実に簡単に書ける
Q. 円 $x^2\!+\!y^2\!=\!r^2$ 上の点P$(x_1,\ y_1)$ における接線 $l$ の方程式は?
[1] Pが両軸上にないとき $(x_1\neq0$ かつ $y_1\neq0$)
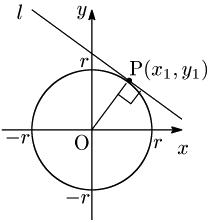
$l$ の傾きを $m$ とすると,OP⊥ $l$ により, \[\frac{y_1}{x_1}\times m=-1\ \ \therefore m=-\frac{x_1}{y_1}\] よって $l$ の方程式は,
\[y-y_1=-\frac{x_1}{y_1}(x-x_1)\]
右辺の分母を払って整理すると
\[x_1x+y_1y={x_1}^2+{y_1}^2\]
Pは円周上の点であるから ${x_1}^2+{y_1}^2=r^2$.よって
\[x_1x+y_1y=r^2\]
[2] Pが軸上にあるとき $(x_1=0$ または $y_1=0$)
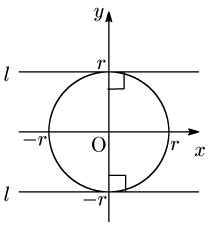
例えば,$x_1=0$ のとき,接点の座標は $(0,\pm r)$ で,接線 $l$ の方程式は \[y=\pm r\] となるが,これは \[0\cdot x\pm r\cdot y=r^2\] と表すことができるので,この場合も[1]に含めることができる.
$y_1=0$ のときも同様に[1]の式でよい.
以上をまとめると,円上の点Pにおける接線の方程式は,Pがその円のどこにあろうと次で書ける:
まとめ 円 $x^2+y^2=r^2$ 上の点P$(x_1,\ y_1)$ における接線 $l$ の方程式は,\[x_1x+y_1y=r^2\]
この結果を見ると,円周上の点 $(x_1,\ y_1)$ における接線の方程式は,円の方程式 $x^2+y^2=r^2$ の左辺を $x\cdot x+y\cdot y=r^2$ と書き換えたうえで,$x$ と $y$ のそれぞれ片側に添え字の1を書き入れるだけで出来上がる.