高校数学[総目次]
数学Ⅱ 第3章 図形と方程式
| スライド | ノート | 問題 | |
| 1. 座標平面上の点 | |||
| 2. 直線の方程式 | |||
| 3. 円の方程式 | |||
| 4. 円と直線 | |||
| 5. 軌跡と方程式 | |||
| 6. 不等式と領域 |

6.不等式と領域
6.1 不等式の表す領域
不等式が領域を表すとはどういうことか
例えば $x,\ y$ を実数として,$y>x+1$ という不等式を満たす $(x,\ y)$ の組にはどんなものがあるだろうか?
\[(x,\ y)=(0,2),\ (0,3),\ (1,6),\ (-4,7),\ \cdots\]
というように考え始めるといくらでもありそうである.そこで今,$x$ の値を例えば3に固定しておいて,そのとき $y$ が満たすべき条件を考えてみると
\[y>3+1=4\ \ \therefore y>4\]
である.つまり
$(x,\ y)=$ ( 3, (4より大きい数) )
という組は不等式 $y>x+1$ を満たすことがわかる.
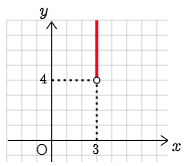
これを他の $x$ の値についても調べてみよう.
$x=-1$ のとき,$y>0$
$x=0$ のとき,$y>1$
$x=1$ のとき,$y>2$
$x=2$ のとき,$y>3$
$\vdots$
これらをグラフに表すと次のようになる:
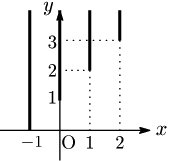
この要領で,もっと細かく調べて,$x$ がすべての実数をとるように動かしていくと,$y>x+1$ 満たす $(x,\ y)$ の組は,1つの領域となって浮かび上がる.それは直線 $y=x+1$ を境界線とする図の斜線領域である.ただし,境界線は含まない.
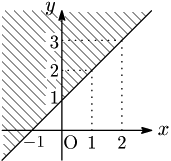
注意
境界線を図示する際の注意点
境界線をかく際には,可能な範囲でそのグラフから方程式が復元できるように通過点などの情報を書き込んでおく.例えば,
直線 :2点
円 :中心と半径がわかるようにしておく
放物線:頂点ともう1点
など.

一般に不等式の表す領域は次のようになる:
[1] $y>f(x)$ の表す領域
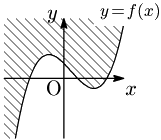
[2] $y< f(x)$ の表す領域
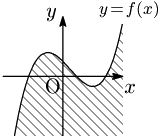
注意
不等式の表す領域は,通常斜線で図示する.その際,境界線を含む,含まないについてのコメントも必ず添えておく.
例題 不等式 $xy>1$の表す領域を図示せよ.
解答例を表示する
\[\left\{\begin{array}{ll}
x>0\, \mbox{のとき}&y>\dfrac1x\\[5pt]
x<0\, \mbox{のとき}&y<\dfrac1x
\end{array}\right.\]
よって,$xy>1$ の表す領域は図の境界線を含まない斜線部分:
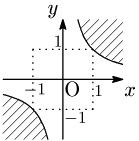
$xy>1$
\[\left\{\begin{array}{ll}
x>0\, \mbox{のとき}&y>\dfrac1x\\[5pt]
x<0\, \mbox{のとき}&y<\dfrac1x
\end{array}\right.\]
よって,$xy>1$ の表す領域は図の境界線を含まない斜線部分:

補足
上の例題と,$y>\dfrac1x$ の表す領域とは異なることに注意.
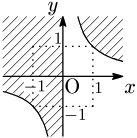
(境界線を含まない)

発展的補足
2点がある直線に関して異なる領域に属することを表現する方法
例えば,$y\boldsymbol{>}x+1$ の表す領域に属する任意の点を $(x_1,\ y_1)$ とすると,$y_1>x_1+1$,即ち \[x_1-y_1+1<0\] が成り立つ.
また,$y\boldsymbol{<}x+1$ の表す領域に属する任意の点を $(x_2,\ y_2)$ とすると,$y_2<x_2+1$,即ち \[x_2-y_2+1>0\] が成り立つ.
つまり,直線 $x-y+1=0$ に関して異なる領域に属する2点の座標を $x-y+1$ に代入すると,式の値は異符号になる.この事実は例えば「直線が座標平面上の2点の間を通過する」といった条件で利用される.

$x>h,\ y>k\ (h,k$ は定数)の表す領域
座標軸に平行な直線が境界線となる場合
特別な場合として,座標軸に平行な直線が境界線となる場合を確認しておこう.
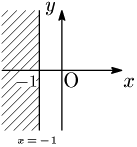
例1 $x<-1$
これは「$x$ 座標が $-1$ より小さい点全体」を意味する.要するに $x$ 座標にだけ条件が付されており,$y$ 座標は自由に取れるということである.すると,そのような点全体の集合は次図のようになる:
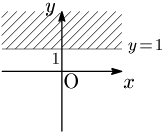
例2 $y\geqq1$
これは「$y$ 座標が1以上である点全体」を意味する.要するに $y$ 座標にだけ条件が付されており,$x$ 座標は自由に取ってよい.すると,そのような点全体の集合は次図のようになる:

6.2 円の内部・外部
円の内部や外部を不等式で表す
円の方程式 のところで,$(x-a)^2+(y-b)^2=r^2$ を満たす点 $(x,\ y)$ の集合は,点 $(a,\ b)$ を中心とする半径 $r$ の円であった.従って $(x-a)^2+(y-b)^2\neq r^2$ であれば,もはや点 $(x,\ y)$ は円周上にはない.ではこのとき点は円の内部にあるのだろうか,外部にあるのだろうか.
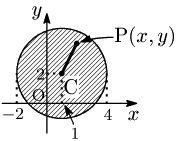
例題 不等式 $(x\!-\!1)^2\!+\!(y\!-\!2)^2\!\leqq\!3^2$ の表す領域を図示せよ.
P$(x,y)$ ,C$(1,2)$ とすると,与式は
\[\begin{align*}
{\rm CP}^2&\leqq3^2\\[5pt]
\therefore {\rm CP}&\leqq3
\end{align*}\]
よって与式を満たすPは,円 $(x\!-\!1)^2\!+\!(y\!-\!2)^2\!=\!3^2$ の周及び内部にある.
従って,与式の表す領域は図の境界線を含む斜線部分である:
一般に次が成り立つ:
円 $(x-a)^2+(y-b)^2=r^2\ \cdots$ ①について,
[1] $(x-a)^2+(y-b)^2<r^2$
→ 円①の内部
[2] $(x-a)^2+(y-b)^2>r^2$
→ 円①の外部
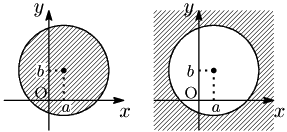
ともに境界線を含まない.
例題 連立不等式$\left\{\begin{array}{l}y> x+1\\x^2+y^2\leqq 4\end{array}\right.$ の表す領域を図示せよ.
解答例を表示する
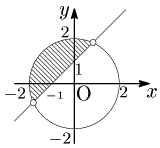
境界線は,円周を含み,直線及び円と直線の交点を含まない


6.3 線形計画法
直線で囲まれた制約領域で最大・最小を考える
2つの材料A,Bを用いて2種類の製品X,Yを作っている工場がある.ただし,材料Aは10個,材料Bは15個しかない.製品Xを1つ作るためには材料Aが2つ,材料Bが1つ必要である.一方製品Yを1つ作るためには材料Aが1つ,材料Bが3つ必要である.まとめると次の表のようになる:
| 製品X | 製品Y | |
| 材料A | 2 | 1 |
| 材料B | 1 | 3 |
2つの製品の価格は共に1個当たり1万円とする.売り上げを最大にするには製品X,Yをそれぞれ何個ずつ作ればよいだろうか.
この問題は,製品X,Yをそれぞれ $x,\ y$ 個ずつ作るとして,次の例題を解くことに帰着される:
例題 $x,y$ が次の不等式 \[\left\{\begin{array}{l}x\geqq0,\ y\geqq0\\ 2x+y\leqq10\\ x+3y\leqq15 \end{array}\right.\] を満たすとき,$x+y$ の最大値と最小値を求めよ.
前提となる考え方
例えば,$x+y=5$ となる $(x,\ y)$ の組は無数にあるが,それらの組1つ1つを座標平面上に落としていくと,やがて1つの図形が浮かび上がる.それは即ち直線 $y=-x+5$ である.この直線上の任意の点 $(x,\ y)$ は,$x+y$ の値が5になるのだ.和が5になる $(x,\ y)$ の組は,漏れなくこの直線上の点として尽くされているのであり,この直線からわずかでもはみ出そうものなら,その点 $(x,\ y)$ は,もはや $x+y$ の値が5にならない.
ここで $x=0$ のペアとなる $y$ の値を調べてみると,$y=-0+5=5$ である.この $(x,\ y)=(0,\ 5)$ という点は,紛れもなく直線が $y$ 軸と交わる点である.かくして $x+y$ がいかなる値であるかを確認する最も手っ取り早い方法は,直線 $x+y=k$ の書き換えである $y=-x+k$ の $y$ 切片を見れば良いことがわかる.
ポイント
$x+y=k$ とおく.
→ 直線を表し,$k$ はその $y$ 切片
境界線の傾きに注意して $k$ を動かす