三角比の相互関係｜sin・cos・tanの最重要公式をスライドでやさしく解説

高校数学[総目次]

数学Ⅰ　第2章　三角比

	スライド	ノート	問題
1. 正接，正弦，余弦
2. 三角比の相互関係
3. 三角比の拡張
4. 正弦定理
5. 余弦定理
6. 三角形の面積

2．三角比の相互関係

2.1　三角比の相互関係

sin, cos, tan は相互に関係がある

　$\sin\theta=\dfrac35$ というとき，直角三角形の $\dfrac{\mbox{高さ}}{\mbox{斜辺}}$ の値が $\dfrac35$ であったということだから，長さの比が (斜辺)：(高さ)＝5：3 である．今例えば斜辺が5，高さが3とすれば，残りの底辺については三平方の定理から $\sqrt{5^2-3^2}=4$ と計算できる．すると，$\sin\theta$ 以外の $\cos\theta,\ \tan\theta$ も，$\cos\theta=\dfrac45$，$\tan\theta=\dfrac34$ と計算できてしまう．

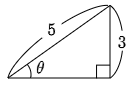
　一般に直角三角形の3つの辺から2つを選ぶ方法は3通りあって，これらの各組から三角比が定義されたのであったから，$\tan \theta,\ \sin\theta,\ \cos\theta$ のどれか1つでもわかっていれば，あとの2つは計算で求めることができてしまう．何故なら残りの1辺は三平方の定理から求めることができ，従ってその直角三角形の3つの辺の長さの比がすべてわかってしまうからだ．

まずは具体例で相互関係を確認

　上の例では $\sin\theta=\dfrac35$ とすれば，それに応じて $\cos\theta,\ \tan\theta$ が決まった．つまり，3つの三角比の間には相互に関係があるのだ．その関係として公式になっているのが3つあるのだが，それをまずは具体例で見ていくとしよう．

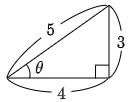
　図のように $\theta$ をとると，$\sin\theta=\dfrac35,\ \cos\theta=\dfrac45,\ \tan\theta=\dfrac34$ であるから

$3=5\sin\theta\ (\cdots$ア), $4=5\cos\theta\ (\cdots$イ), $\tan\theta\!=\!\dfrac34$

である．三平方の定理により $3^2+4^2=5^2$ が成り立つから，左辺の 3 と 4 を (ア)，(イ) に置き換えて

$$(5\sin\theta)^2+(5\cos\theta)^2=5^2$$

$$5^2(\sin\theta)^2+5^2(\cos\theta)^2=5^2$$

　両辺を $5^2$ で割ると

$$\sin^2\theta+\cos^2\theta=1$$

が成り立つ．

※　$(\sin\theta)^n$ はしばしば $\sin^n\theta$ と表される．$\cos\theta$ や $\tan\theta$ も同様．

次に， $\tan\theta=\dfrac34$ について，右辺の分母子を (ア)，(イ) で置き換えると

$$\tan\theta=\dfrac{5\sin\theta}{5\cos\theta}$$

　右辺の5を約分して

$$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$$

　最後に先ほど得られた $\sin^2\theta+\cos^2\theta=1$ の両辺を $\cos^2\theta$ で割ると

$$\begin{align*} \dfrac{\sin^2\theta}{\cos^2\theta}+1&=\dfrac1{\cos^2\theta}\\[5pt] \therefore\ \ \left(\dfrac{\sin\theta}{\cos\theta}\right)^2+1&=\dfrac1{\cos^2\theta} \end{align*}$$

　左辺にすぐ上で得られた $\tan\theta$ の式を代入して

$$1+\tan^2\theta=\dfrac1{\cos^2\theta}$$

　これら3つの関係式が最重要なものとして今後大活躍することになる．

それではここから相互関係の一般論

　上の例と同様にして，一般の場合の三角比の相互関係を導いてみよう．