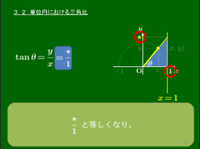
鈍角の三角比が何を意味するのか,スライドで大変わかり易く解説しています.これまで理解できなかった人でも,スライドを見れば必ず納得できるはずです.是非ご覧ください!
このページにある内容は,こちらのスライド(会員向け)でわかり易く説明しています.
※PC環境なら全画面表示でより見やすく,よりわかりやすい!
高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | |||
| 2. 三角比の相互関係 | |||
| 3. 三角比の拡張 | |||
| 4. 正弦定理 | |||
| 5. 余弦定理 | |||
| 6. 三角形の面積 |

3.三角比の拡張
0°や180°までの角にも三角比を定義したい
直角三角形の直角以外の角に対して三角比 sin, cos, tan は定義された.これらは直角三角形の存在を前提としていたから,当然ながらその角は $0^\circ<\theta<90^\circ$ である.ここではこの角を $0^\circ$ や $90^\circ$ 以上にまで拡張するのが1つの目的である.しかし直角以外の内角が $0^\circ$ や $90^\circ$ 以上ではもはや直角三角形を作ることはできない.こういった角に対して三角比を考えるには,直角三角形の存在を前提としていたこれまでの定義そのものを見直さなければならない.ただ見直すといっても例えば $\sin30^\circ=\dfrac12$ や $\cos45^\circ=\dfrac{\sqrt2}2$ といった,これまでの定義で定められた値はそのままにしておきたい.そのままにした上で,$0^\circ$ や $90^\circ$ 以上の角に対して sin, cos, tan の値を定義できるような純然たる拡張を考えるのである.その拡張のアイデアとは一体どのようなものなのだろうか.
3.1 座標を用いた三角比の定義
三角比拡張のアイデア
冒頭で述べた拡張のアイデアとは,
座標軸を導入し,原点を中心とする半径 $\boldsymbol{r}$ の半円で考える
ことなのである.
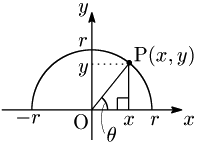
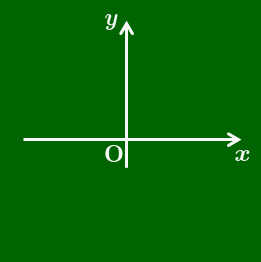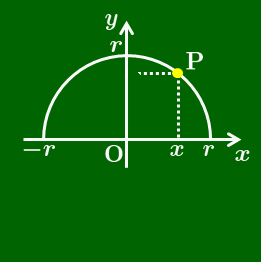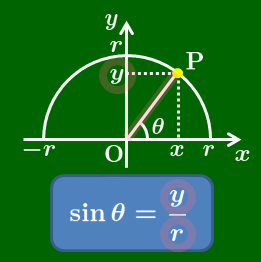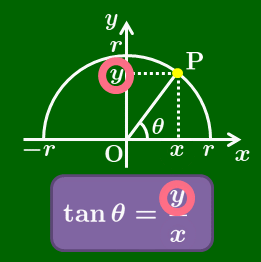
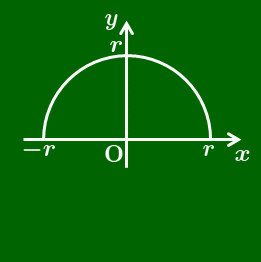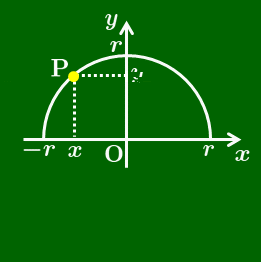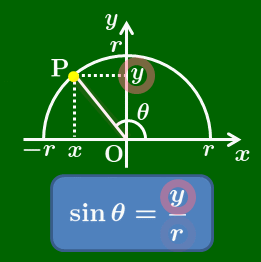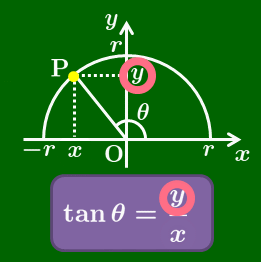
原点Oを中心とする半径 $r$ の円周上に点Pがあり,その座標を $(x,\ y)$ とする.線分OPが $x$ 軸の正の向きとのなす角を $\theta$ とすると,三角比 $\sin\theta$,$\cos\theta$,$\tan\theta$ を次のように定義し直す:
θ が鋭角のとき
\[\begin{align*}
\sin\theta=\frac yr\\[5pt]
\cos\theta=\frac xr\\[5pt]
\tan\theta=\frac yx
\end{align*}\]
$\theta$ が鋭角のとき
そしてこの定義を,そのまま $\theta$ が鈍角の場合に対しても適用するのである:
θ が鈍角のとき
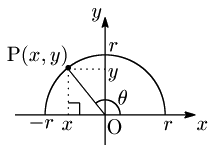
\[\begin{align*}
\sin\theta=\frac yr\\[5pt]
\cos\theta=\frac xr\\[5pt]
\tan\theta=\frac yx
\end{align*}\]
$\theta$ が鈍角のとき
$\theta=0^\circ,\ 90^\circ,\ 180^\circ$ のときも同様に定義すると,$0\leqq \theta\leqq180^\circ$ の三角比は次のようになる:
0°から180°までの三角比
原点Oを中心とする半径 $r$ の円周上にある点をP$(x,\ y)$ とし,OPと $x$ 軸の正の向きとのなす角を $\theta$ とすると,
\[\begin{align*} &\sin\theta=\frac yr\\[5pt] &\cos\theta=\frac xr\\[5pt] &\tan\theta=\frac yx \end{align*}\]

従来の三角比との違いは何か
この定義において,従来の直角三角形を前提としていた三角比の定義からの変更点は次の通りである.
これまで 変更後
$\sin:\hspace{10mm}\dfrac{\mbox{高さ}}{\mbox{斜辺}}\ \ \to\ \ \dfrac{{\rm P} \mbox{の}\,y\,\mbox{座標}}{\mbox{半径}}$
$\cos:\hspace{10mm}\dfrac{\mbox{底辺}}{\mbox{斜辺}}\ \ \to\ \ \dfrac{{\rm P} \mbox{の}\,x\,\mbox{座標}}{\mbox{半径}}$
$\tan:\hspace{10mm}\dfrac{\mbox{高さ}}{\mbox{底辺}}\ \ \to\ \ \dfrac{{\rm P} \mbox{の}\,y\,\mbox{座標}}{{\rm P} \mbox{の}\,x\,\mbox{座標}}$
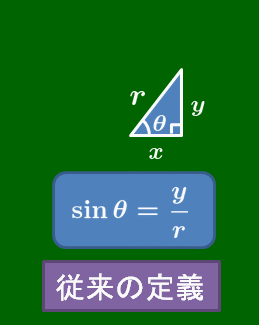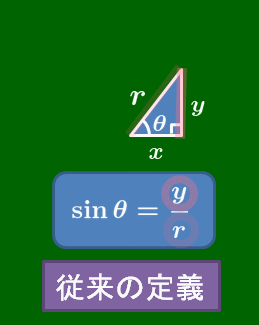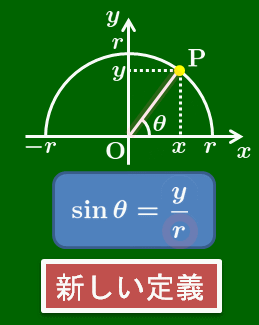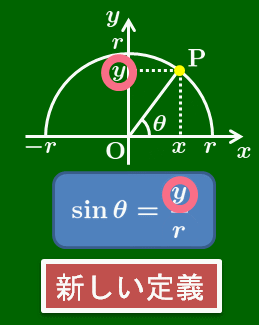
この変更方法は,直角三角形を存在を前提として定義された値はそのままに,$0^\circ$ や $90^\circ$ 以上の角まで定義できるようなものになっている.実に見事な拡張であるといえる.
例1 $\theta=120^\circ$