高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | |||
| 2. 三角比の相互関係 | |||
| 3. 三角比の拡張 | |||
| 4. 正弦定理 | |||
| 5. 余弦定理 | |||
| 6. 三角形の面積 |
演習問題
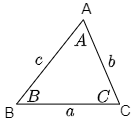
※以下の問題では,△ABCにおいて下図のように∠A,∠B,∠Cをそれぞれ $A,B,C$ (斜体)で表し,辺BC,CA,ABをそれぞれ $a,b,c$ (小文字の斜体)で表すものとする.
問題1【基本】 ヒント
△ABCにおいて,$a=\sqrt 2,b=5, A=135^\circ$ のとき,$C$ を求めよ.
問題2【基本】 ヒント
△ABCにおいて,$\sin A:\sin B:\sin C=5:7:8$ のとき,$a:b:c$ を求めよ.
問題3【基本】 ヒント
△ABCにおいて,$A:B:C=1:2:3$ のとき,$A,B,C$ 及び $a:b:c$ を求めよ.
問題4【標準】 ヒント
△ABCにおいて,次の関係が成り立つとき,△ABCはどのような形の三角形か.\[a\sin A=b\sin B\]
解答
正弦定理により
\[\frac{5\sqrt2}{\sin135^\circ}=\frac5{\sin B}\]
よって
