高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | |||
| 2. 三角比の相互関係 | |||
| 3. 三角比の拡張 | |||
| 4. 正弦定理 | |||
| 5. 余弦定理 | |||
| 6. 三角形の面積 |

5.余弦定理
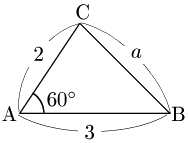
正弦(sin)に関する定理(正弦定理 )があったように,余弦(cos)に関する定理も存在し,余弦定理と呼ばれている.余弦定理の典型的な利用場面としては,例えば次の図のように,三角形の2辺とその間の角が与えられたとき,残りの辺の長さである $a$ を求めたいといった状況がその一例となる.
5.1 余弦定理
余弦定理とは
△ABCにおいて,3辺の長さと1つの角の大きさについて,次の余弦定理と呼ばれる関係が成り立つ:
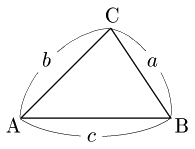
\[\begin{align*}
a^2&=b^2+c^2-2bc\cos A\\[5pt]
b^2&=c^2+a^2-2ca\cos B\\[5pt]
c^2&=a^2+b^2-2ab\cos C
\end{align*}\]
この定理により,三角形の3つの辺の長さと1つの角の大きさの合計4つの要素のうち,3つがわかっていれば,残り1つも求めることができる.ただし,わかっている3つの組合せによっては残り1つが1通りに定まらないこともある.その場合でも条件から更に吟味してどちらかに定められることもある.
証明の方針
$\boldsymbol{a^2=b^2+c^2-2bc\cos A}$ を示す場合
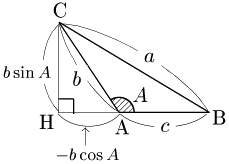
1.Cから直線ABに垂線CHを下ろす.
↓
2.△CBHで三平方の定理を利用.
∠Aが鋭角・直角・鈍角で3通りの場合分け
証明
$a^2=b^2+c^2-2bc\cos A$ を示す.
$A$ が鋭角,直角,鈍角の3通りで場合分けする.
1° $A$ が鋭角のとき
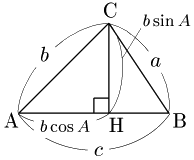
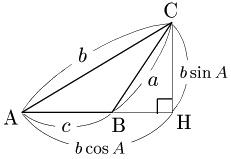
Cから辺ABまたはその延長上に垂線CHを引く.$B$ が鋭角,または鈍角のときは,△CBHにおいて三平方の定理により, \[{\rm CB}^2={\rm BH}^2+{\rm CH}^2\] \[\therefore a^2=|c-b\cos A|^2+(b\sin A)^2\] が成り立つ.$B$ が直角の場合は△CBHがつぶれてしまうが, $a=b\sin A$,$c=b\cos A$ であるから上の式はこの場合も含まれる.この式の右辺は \[\begin{align*} &(c^2-2bc\cos A+b^2\cos^2A)+b^2\sin^2A\\[5pt] =&b^2(\sin^2A+\cos^2A)+c^2-2bc\cos A\\[5pt] =&b^2+c^2-2bc\cos A \end{align*}\] となるから, \[a^2=b^2+c^2-2bc\cos A\] が成り立つ.
2° $A$ が直角のとき
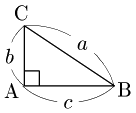
$\cos A=\cos90^\circ=0$ であるから,
\[a^2=b^2+c^2-2bc\cos90^\circ\]
すなわち
\[a^2=b^2+c^2\]
を示せばよいが,三平方の定理によりこれは成り立つ.
3° $A$ が鈍角のとき