スライド ノート 問題
1. 正接，正弦，余弦 [無料]   [会員]
2. 三角比の相互関係 [無料]   [会員]
3. 三角比の拡張 [会員]    
4. 正弦定理 [会員]   [会員]
5. 余弦定理 [会員]   [会員]
6. 三角形の面積 [会員]   [会員]

演習問題

※以下の問題では，△ABCにおいて下図のように∠A，∠B，∠Cをそれぞれ $A,B,C$ (斜体)で表し，辺BC，CA，ABをそれぞれ $a,b,c$ (小文字の斜体)で表すものとする．

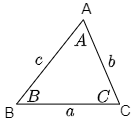
問題１【基本】　　ヒント　ヒント
　次の条件を満たす△ABCは，どのような形の三角形か．\[\sin A=2\cos B\sin C\]

問題２【標準】　　ヒント　ヒント
　△ABCにおいて，次の等式を証明せよ．\[a\cos A\sin C=(b-a\cos C)\sin A\]

問題３【標準】　　ヒント
　1辺の長さが2である正四面体OABCにおいて，辺OAの中点をMとする．辺BC上に点Pをとるとき，線分PMの長さの最小値を求めよ．

問題１【基本】

　次の条件を満たす△ABCは，どのような形の三角形か．\[\sin A=2\cos B\sin C\]

解答

　 POINT
　三角比は正弦定理，余弦定理を用いてすべて辺の長さの式にするのが定石です．

　△ABCの外接円の半径を $R$ とすると，

正弦定理により　$\sin A=\dfrac a{2R},\ \sin C=\dfrac c{2R}$
余弦定理により　$\cos B=\dfrac{c^2+a^2-b^2}{2ca}$