このページにある内容は,こちらのスライド(会員向け)でわかり易く説明しています.
高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | |||
| 2. 三角比の相互関係 | |||
| 3. 三角比の拡張 | |||
| 4. 正弦定理 | |||
| 5. 余弦定理 | |||
| 6. 三角形の面積 |

6.三角形の面積
6.1 三角形の面積
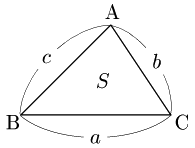
次のような△ABCの面積を求めてみよう.
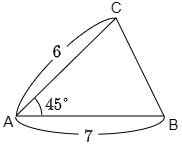
辺ABを底辺と見れば,面積を求めるために必要な情報は高さである.高さを求めるために頂点Cから辺ABに垂線CHを引くと,△ABCの面積は $\dfrac12{\rm AB\cdot CH}$ で求められる.
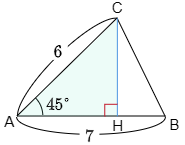
CHの長さは,直角三角形ACH(水色)で考えると,直角三角形の辺の長さをsinで表す公式 より $\rm{CH=AC\,sin45^\circ}$ となるから,
この下線部分の式こそが,これから学ぼうとしている三角形の面積を表す公式なのである.
sinを用いた三角形の面積の公式
△ABCにおいて,頂点A,B,Cに対応する辺の長さをそれぞれ $a$,$b$,$c$ とする.
Cから直線ABに垂線CHを引くと,$A$ が鋭角・鈍角のいずれであっても $\sin A>0$ であるから,CHの長さは $b\sin A$ で表される:
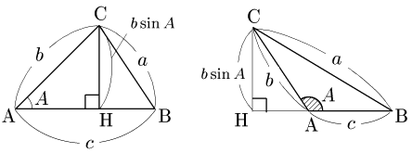
三角形の面積は,$\dfrac12$×(底辺)×(高さ) で求められるから,△ABCの面積を $S$ とすると
\[S=\frac12\cdot{\rm AB}\cdot{\rm CH}=\frac12bc\sin A\]
となる.この式から三角形の面積を知るには,2辺の長さとその間の sin の値がわかればよいということがわかる.今,2辺とその間の角として,$b$,$c$,$A$ を選んだが,他にも $c$,$a$,$B$ という組と,$a$,$b$,$C$ という組がある.
三角形の面積 △ABCの面積 $S$ は,
\[S=\frac12 bc\sin A=\frac12 ca\sin B=\frac12 ab\sin C\]

例題 △ABCにおいて,$a=5,\ b=7,\ c=3$ のとき,△ABCの面積 $S$ を求めよ.
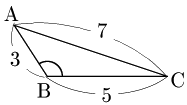
こたえ

6.2 ヘロンの公式
三角形の3辺の長さを用いた三角形の面積の公式
三角形の3辺の長さがわかっているときに,面積を求める公式が存在する.3辺の長さを $a, b, c$ とし
\[s=\frac{a+b+c}2\]
で定められる $s$ を用いて表される次の公式をヘロンの公式という.
ヘロンの公式 $s$ (小文字) を $s=\dfrac{a+b+c}2$ とすると,△ABC の面積 $S$ (大文字)は,
\[S=\sqrt{s(s-a)(s-b)(s-c)}\]

この公式は,形こそきれいであるものの,$a,b,c$ が整数や簡単な分数でない限りは $s$ が簡単な値にはならず,その $s$ を用いた根号の中身の計算も複雑になりがちであるせいか,使える場面はそれほど多くないように感じる.加えて,三角形の面積を求める他の公式でよく登場する $\dfrac12$ がないことや,$s$ は $a,b,c$ の3つの数を加えた上で3ではなく2で割ることなど,色々とうっかりしてしまいそうな点があることにも注意しなければならない.
証明
余弦定理により,$\cos A=\dfrac{b^2+c^2-a^2}{2bc}$.
よって,