高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | 問題 | |
| 1. 一般角と弧度法 | |||
| 2. 一般角の三角関数 | |||
| 3. 三角関数の性質 | |||
| 4. 三角関数のグラフ | |||
| 5. 三角関数の加法定理 | |||
| 6. 三角関数の種々の公式 | |||
| 7. 三角関数の合成 | |||
| 8. 三角関数の応用 |

1.一般角と弧度法
1.1 一般角とは
まずは一般角のイメージを
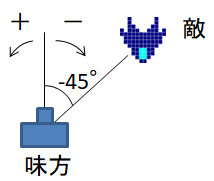
例えば,図のようなインベーダーゲームにおいて,自分は司令塔にいるとする.向かいくる敵を迎撃するにはどの方向に大砲を向ければよいかの指令を出すのに,真正面を基準線とし,反時計回りを「+」,時計回りを「-」として「-45°に撃て!」と指示すればよいだろう.また,敵が自分たちの周りを反時計回りに旋回して2回転したとき,「敵は+720°移動した」ということもできよう.一般角とは大雑把に言えばこのような角の表現のことである.

一般角とは何か,これまでの角との違いは?
これまで角といえばその大きさのみが問題であった.これからは大きさに加え,向きも考慮に入れた角を考えることにする.
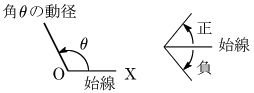
半直線OXはOを中心に回転するとする.この動く半直線を動径といい,スタートラインを始線という.そして始線から反時計回りに回転したときにできる角を正の角,時計回りに回転したときにできる角を負の角という.
このように,始線からの回転の向きと大きさを表した角を一般角という.また始線からの角が $\theta$ である動径を $\boldsymbol{\theta}$ の動径という.
一般角とは単に大きさだけでなく回転の向きも表した角
+と-は正負ではなく,回転の向きを意味する
正の角は例えば $+60^\circ$ のように記号「+」を用いて表されるが,通常この「+」は省略される.また逆に負の角は $-60^\circ$ のように記号「-」を用いて表され,こちらは省略できない.このように「-」の記号を用いて「負」の角と呼ぶなど実数と同じ表現を用いて紛らわしいが,記号「-」は負の数を意味を表すのではなく,動径が回転する向きを表すのだということに十分注意しておく必要がある.
注意
動径は$360^\circ$で元の位置に戻るから,角 $\theta$ の動径と,角 $(\theta+360^\circ\times n)\ (n$ は整数) の動径は一致する.
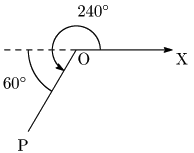
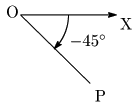
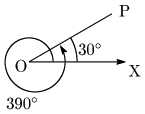
例題 次の角の動径OPを図示せよ.
(1) $240^\circ$ (2) $-45^\circ$ (3) $390^\circ$
こたえ
(1)
(2)
(3)

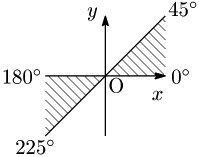
1.2 象限の角
角 $\theta$ について,$n$ を整数として
\[\theta=\alpha+360^\circ\times n\]
と表されるとき,次のような「第○象限の角」という表現がしばしば用いられる.
象限の角 $\theta$ が第1象限の角 $\iff\hspace{3mm}0^\circ<\alpha<90^\circ$
$\theta$ が第2象限の角 $\iff\hspace{1mm} 90^\circ<\alpha<180^\circ$
$\theta$ が第3象限の角 $\iff 180^\circ<\alpha<270^\circ$
$\theta$ が第4象限の角 $\iff 270^\circ<\alpha<360^\circ$
これは要するに,その角の動径が第何象限にあるかということである.
細かな注意であるが,象限の角といったときには境界である $0^\circ$,$90^\circ$,$180^\circ$,$270^\circ$ ,$360^\circ$ 等は除かれる.すなわち動径が $x$ 軸上もしくは $y$ 軸上にある角は,どの象限にも属さないとするのである.
例題 $\theta$ が第1象限の角のとき,$\dfrac\theta2$ は第何象限の角か.
答

1.3 弧度法
弧度法とは
小学生の時から慣れ親しんだ角は,1周りを360等分した大きさを1単位とするもので,度数法と呼ばれる.しかし角を測るのにどうしても360等分しなければならないという理由はない.そこでいま新しい角の計測法を導入する.
半径 $r$ の円で,弧の長さが $r$ のときの中心角を1ラジアンとする角の表し方を弧度法(こどほう)という.この角の表現法は,今後の数学においてとても重要なもので,とりわけ微積分の分野では角度といえば弧度法である.
弧度法とは 半径 $r$ の円において,弧の長さが $r$ のときの中心角を1ラジアンとする角の表し方
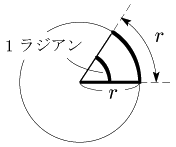
※スライド に1ラジアンの理解を助ける簡単なアニメーションがあります.
この1ラジアンという単位は,半径 $r$ の長さに依存しない.つまり $r=1$ の円で考えようが, $r=100$ の円で考えようが,1ラジアンといえば同じ大きさの角となる.念のために理由を説明しておくと,半径 $r$ の扇形の中心角と弧の長さは比例するから,1周360°に対する1ラジアンの割合は $\dfrac r{2\pi r}=\dfrac1{2\pi}\fallingdotseq\dfrac1{6.28}$ であり,半径 $r$ の値によらない.この割合を用いれば,1ラジアンは
\[360^\circ\times\dfrac1{6.28}\fallingdotseq 57.3^\circ\]
ということになる.

重要例題 180$^\circ$ は何ラジアンか.