高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | 問題 | |
| 1. 一般角と弧度法 | |||
| 2. 一般角の三角関数 | |||
| 3. 三角関数の性質 | |||
| 4. 三角関数のグラフ | |||
| 5. 三角関数の加法定理 | |||
| 6. 三角関数の種々の公式 | |||
| 7. 三角関数の合成 | |||
| 8. 三角関数の応用 |

2.一般角の三角関数
2.1 三角関数の定義
三角関数とは何か
数学Ⅰの三角比のところで,角 $\theta$ を $0^\circ$ や $90^\circ$ 以上に拡張した際のアイデアは,そのまま一般角 $\theta$ に対する $\sin$,$\cos$,$\tan$ に適用することができる.
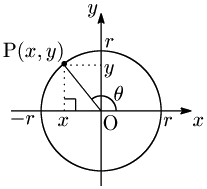
$x$ 軸の正の向きを始線とする一般角 $\theta$ の動径と,原点を中心とする半径 $r$ の円との交点をPとし,その座標を $(x,\ y)$ とする.このとき,$\sin\theta$,$\cos\theta$,$\tan\theta$ を次で定義する:
三角関数の定義
\[\begin{align*}
\sin\theta&=\frac yr\\[5pt]
\cos\theta&=\frac xr\\[5pt]
\tan\theta&=\frac yx\ \ (\theta\neq\frac\pi2+n\pi,\ n\,\mbox{は整数})
\end{align*}\]
この定義によれば,$\sin\theta$,$\cos\theta$,$\tan\theta$ の各値は,相似な図形を考えればわかるように半径 $r$ にはよらず,$\theta$ によってただ1つ定まる.つまり角 $\boldsymbol{\theta}$ の関数である.これら $\sin\theta$,$\cos\theta$,$\tan\theta$ を三角関数という.
例 $\theta=-\dfrac\pi3$ のときの,$\sin\theta$,$\cos\theta$,$\tan\theta$
答 $-\dfrac\pi3$ の動径と,半径2の円との交点をPとすると,Pの座標は $(1,-\sqrt3)$ であるから,
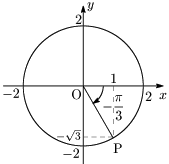
\[\begin{align*} &\sin\left(-\frac\pi3\right)=\frac{-\sqrt3}2=-\frac{\sqrt3}2\\[5pt] &\cos\left(-\frac\pi3\right)=\frac12\\[5pt] &\tan\left(-\frac\pi3\right)=\frac{-\sqrt3}1=-\sqrt3 \end{align*}\]
代表的な三角関数の値をまとめると次の表のようになる:
| $\theta$ | 0 | $\dfrac\pi6$ | $\dfrac\pi4$ | $\dfrac\pi3$ | $\dfrac\pi2$ |
| $\sin\theta$ | 0 | $\dfrac12$ | $\dfrac1{\sqrt2}$ | $\dfrac{\sqrt3}2$ | 1 |
| $\cos\theta$ | 1 | $\dfrac{\sqrt3}2$ | $\dfrac1{\sqrt2}$ | $\dfrac12$ | 0 |
| $\tan\theta$ | 0 | $\dfrac1{\sqrt3}$ | 1 | $\sqrt3$ | – |
| $\theta$ | $\dfrac\pi2$ | $\dfrac{2\pi}3$ | $\dfrac{3\pi}4$ | $\dfrac{5\pi}6$ | $\pi$ |
| $\sin\theta$ | 1 | $\dfrac{\sqrt3}2$ | $\dfrac1{\sqrt2}$ | $\dfrac12$ | 1 |
| $\cos\theta$ | 0 | $-\dfrac12$ | $-\dfrac1{\sqrt2}$ | $-\dfrac{\sqrt3}2$ | 0 |
| $\tan\theta$ | – | $-\sqrt3$ | $-1$ | $-\dfrac1{\sqrt3}$ | 0 |

2.2 単位円における三角関数
三角関数は単位円で考えるのが基本
原点を中心とする半径1の円を単位円という.
単位円で三角関数を考えると,半径 $r=1$ であるから次のようになる:
単位円での三角関数
\[\begin{align*}
\sin\theta&=y\\[5pt]
\cos\theta&=x\\[5pt]
\tan\theta&=\frac yx
\end{align*}\]
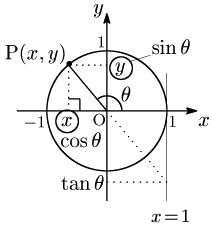
今後三角関数は基本的に単位円を用いて考えていくことになる.その理由は何か.単に $\sin\theta,\cos\theta$ が分数の表記を取らないからラクだというのは些細なメリットで,それよりずっと大きなメリットは図のように角 $\theta$ の動径をOPとすると,
${\boldsymbol \sin\theta}$ はPの ${\boldsymbol y}$ 座標そのもの
${\boldsymbol \cos\theta}$ はPの ${\boldsymbol x}$ 座標そのもの
となることである.つまり
三角関数を単位円で考えることの意義$\boldsymbol{\sin\theta,\ \cos\theta}$ の視覚化
であり,これは誠に重要である.

