高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | 問題 | |
| 1. 一般角と弧度法 | |||
| 2. 一般角の三角関数 | |||
| 3. 三角関数の性質 | |||
| 4. 三角関数のグラフ | |||
| 5. 三角関数の加法定理 | |||
| 6. 三角関数の種々の公式 | |||
| 7. 三角関数の合成 | |||
| 8. 三角関数の応用 |

4.三角関数のグラフ
4.1 $\sin\theta$ のグラフ
$\sin\theta$ のグラフとは
$y=\sin\theta$ のグラフとはどのようなものであろうか.$y=x+1$ であれば, $x$ の各値に対して $y$ がただ一つ定まり,その $(x,y)$ の組を座標平面にかいていけばよいのであり,特段難しいところはないであろう.これと同じことを $y=\sin\theta$ でも考えて,各 $\theta$ の値に対してただ一つ定まる $y$ の値を組にして, $(\theta, y)$ を座標平面にかいていけばよいのだ. $\theta$ が文字としてとっつきにくいなら横軸を $x$ に代えて $y=\sin x$ のグラフを考えてもよい.
注意しておかなければならないのは,角度を表す $\theta$ は弧度法を用いるということである.度数法と弧度法の換算は
180° = $\pi$ ラジアン
である.別の書き方をすれば
180° = 3.1415 … ラジアン
となる.従って,
| $\theta$ | 0 | $\dfrac\pi6$ | $\dfrac\pi4$ | $\dfrac\pi3$ | $\dfrac\pi2$ |
| $\sin\theta$ | 0 | $\dfrac12$ | $\dfrac{\sqrt2}2$ | $\dfrac{\sqrt3}2$ | 1 |
というのは
| $\theta$ | 0 | $0.52\cdots$ | $0.78\cdots$ | $1.04\cdots$ | $1.57\cdots$ |
| $\sin\theta$ | 0 | $\dfrac12$ | $\dfrac{\sqrt2}2$ | $\dfrac{\sqrt3}2$ | 1 |
と表すこともできる.
$\sin\theta$ のグラフは曲線となるから,グラフを描くときはできるだけ多くの $\theta$ とその値に対する $\sin\theta$ の値をとってプロットした方が正確な図が描ける.しかしながら上の表にあるようないくつかの $\theta$ の値以外の $\sin\theta$ の値を計算することは簡単ではない.この辺りの事情は,同じようにグラフが曲線となる $y=x^2$ などのグラフをかく場合と著しく異なる.
$\sin\theta$ のグラフをコンピュータで描いてみる
下のアニメーションは,
$\sin\theta$ は単位円周上の点の $y$ 座標である
という事実を用いてグラフを描く方法である.
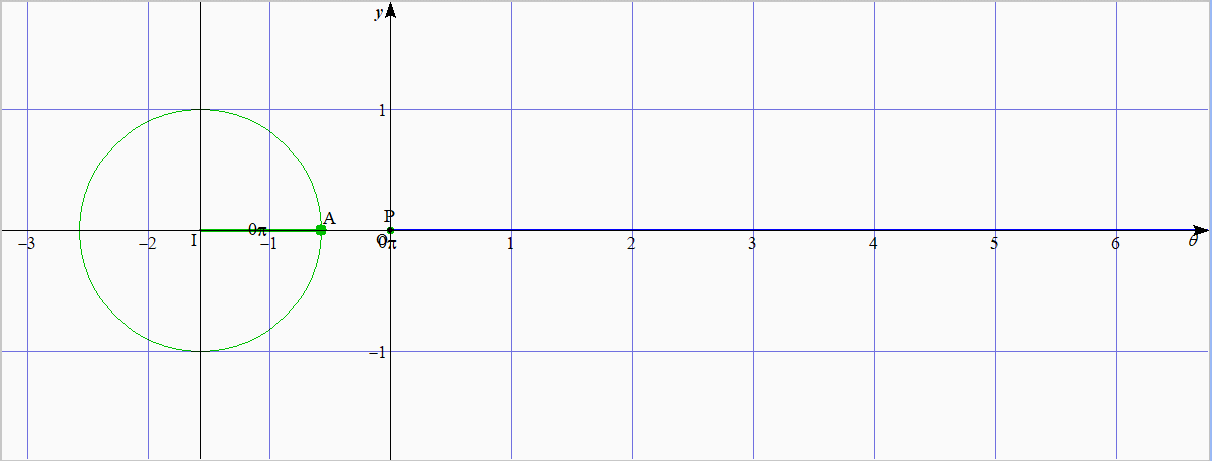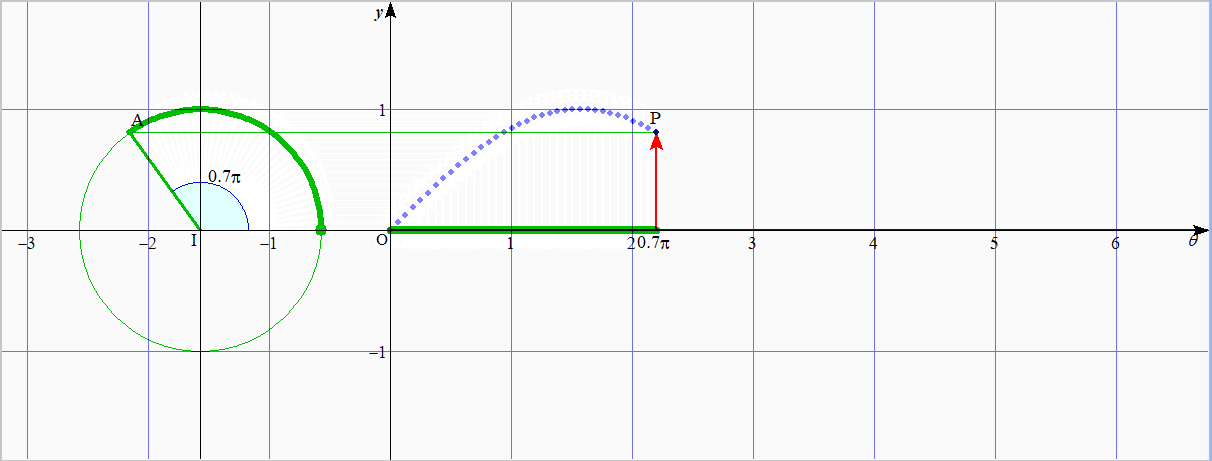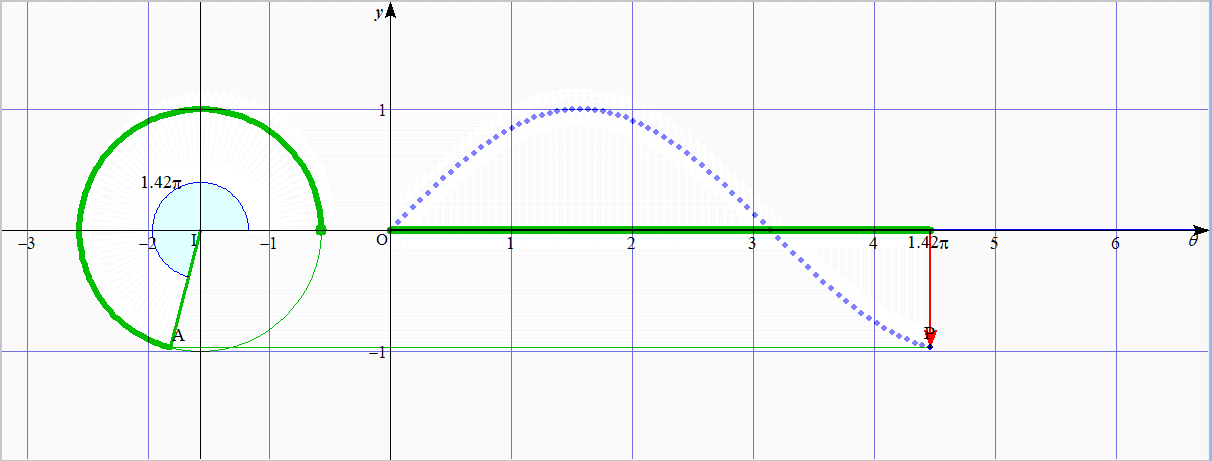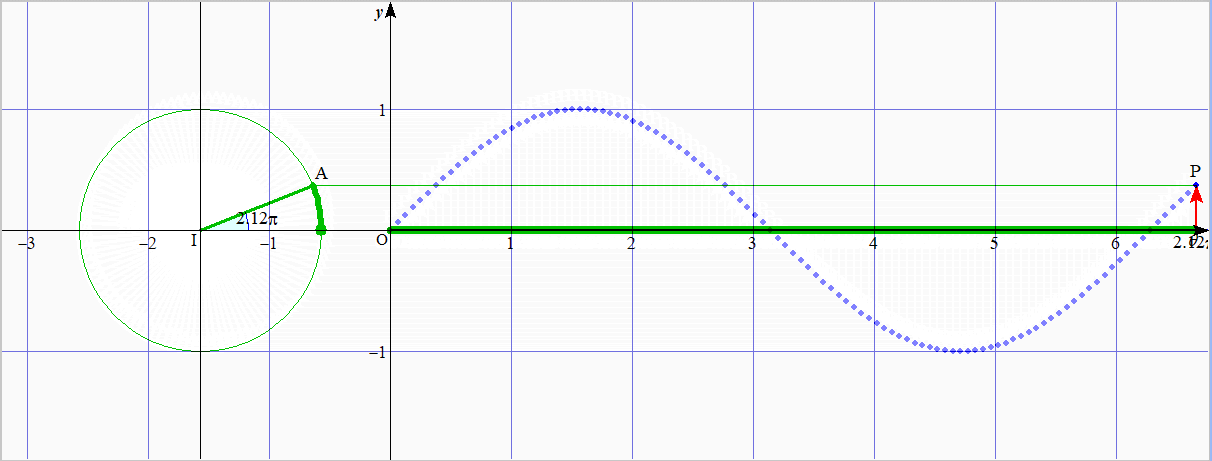
緑色の太線が同じ長さ
$y=\sin\theta$ のグラフのかき方は,スライド(会員向け)でもパラパラ漫画的にわかりやすく解説しています.
実際に人が手でグラフをかく場合には,アニメーションのような手法で厳密にグラフを描くことは困難なので,私たちがよく知っているいくつかの $\theta$ に対する $\sin\theta$ の値を取り,あとは滑らかに連結することで済ませることが多い.
単位円では中心「角」と弧の「長さ」が等しい
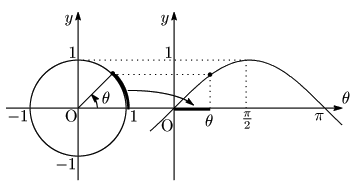
弧度法では,単位円(半径1の円)における中心角とそれに対応する弧の長さが等しい.つまり中心角が $\theta$ なら弧の長さも $\theta$ である(※注).下の図は,弧の長さをそのまま $x$ 軸上にもってくれば $\theta$ の値が取れることを示したものであり,上のアニメーションでは緑色の線がそれを表す.
※注 これは弧度法の定義 である.例えば中心角 $\dfrac\pi4$ の弧の長さは $\dfrac\pi4$,中心角 $\dfrac\pi2$ の弧の長さは $\dfrac\pi2$ 等々.
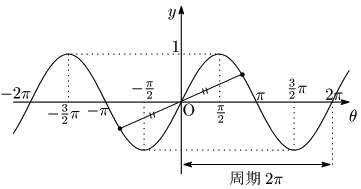
$y=\sin\theta$ のグラフは原点に関して対称
$y=\sin\theta$ のグラフは原点に関して対称となっている.これは奇関数に見られる特徴である.また,$\sin\theta$ の周期は $2\pi$ であるから $2\pi$ ごとにグラフが繰り返される.

4.2 $\cos\theta$ のグラフ
$\cos\theta$ のグラフとは
$y=\cos\theta$ のグラフのかき方は,スライド(会員向け)でパラパラ漫画的にわかりやすく解説しています.
$\cos\theta$ は単位円周上の点の $x$ 座標であった.従って $\sin\theta$ のときと同じように描こうとすると,元となる単位円を反時計回りに90°回転させなくてはならない.それを避けるために,$\cos\theta$ の値からではなく,$y=\cos\theta=\sin\left(\theta+\dfrac\pi2\right)$ の関係を利用した次のような作図法が考えられている.$\sin$ の値は単位円周上の点の $y$ 座標であるから,$\sin\left(\theta+\dfrac\pi2\right)$ の値をそのまま水平右側にもっていけば,$\cos\theta$ の値が得られるという訳である.
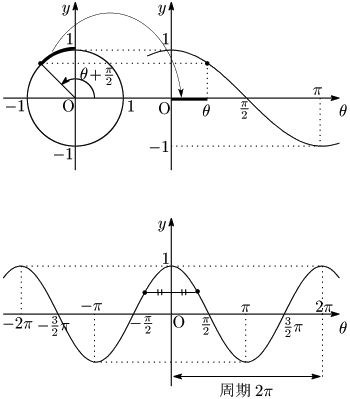
下:$y=\cos\theta$ のグラフ
グラフは $y$ 軸対称