高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | ||
| 2. 関数のグラフの移動 | |||
| 3. 2次関数の最大・最小 | |||
| 4. 2次関数の決定 | |||
| 5. 2次関数のグラフと方程式 | |||
| 6. 2次不等式とグラフ | |||
| 7. 2次方程式の解の配置 |

演習問題
基礎から応用・発展まで幅広く問題を取り揃えました.最後の問題12だけは考えにくい難問で,東大に合格するような人の中でも解けるのは3人に1人もいないのではないでしょうか.
問題1【基本】
次の2次関数に最大値,最小値があればそれを求めよ.最大値または最小値をとるときの
(1)
問題2【基本】
次の2次関数に最大値,最小値があればそれを求めよ.最大値または最小値をとるときの
(1)
(2)
問題3【標準】
(1) 最小値及び最小値をとるときの
(2) 最大値及び最大値をとるときの
問題4【標準】
(1) 最小値及び最小値をとるときの
(2) 最大値及び最大値をとるときの
問題5【標準】
(1) 最小値及び最小値をとるときの
(2) 最大値及び最大値をとるときの
問題6【標準】
(1)
(2)
問題7【標準】
関数
問題8【標準】
関数
問題9【発展】
問題10【発展】
問題11【発展】
(1) 関数
(2) 関数
問題12【難】
関数

2次関数の最大・最小問題を解くときにはいつでもグラフをイメージしながらが考えることが大切です.まずは
下に凸か,上に凸か
です.これがわかったら
軸に関して対称
であることを常に意識しながら考えていきます.
解答
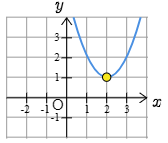
(1)
最大値は ない
最小値は
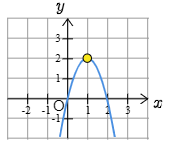
(2)
最大値は
最小値は ない
問題となっている関数は問題1と同じです.問題1では定義域が実数全体の場合で,2次の係数が正だと最小値は存在しますが,最大値の方はいくらでも大きくなるため存在しませんでした.問題2では定義域に制限があり,この場合ですと最大値と最小値を共に持つ可能性があります.ここでもグラフをイメージすることが欠かせません.まずは
軸が定義域に含まれるかどうか
です.
①YES → 軸のところで最大or最小
②NO → 定義域の両端のところで最大と最小
更に①では定義域の両端での値の大小を判定しますが,その際の視点は
どちらがより軸から遠いか
です.
(2)では区間の片方の端である
解答
(1)
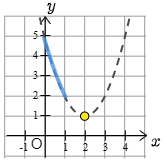
問題1より
となります.
(2)
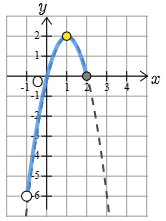
問題1より
最小値は ない
となります.
定義域の左端は0に固定されています.右端の
①下に凸か,上に凸か
②軸は定義域に含まれているか
③軸からより遠い(近い)のはどこか
をグラフとともにイメージすることです.
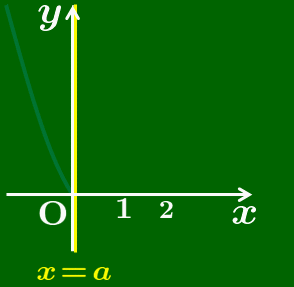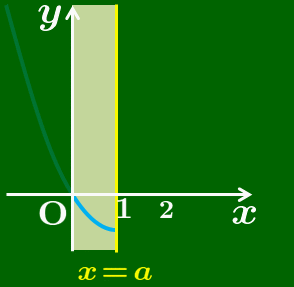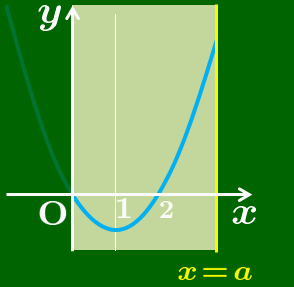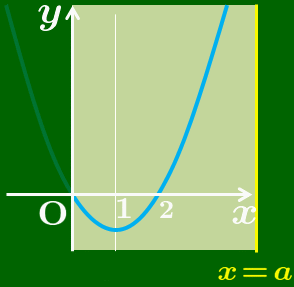
青色のグラフが見えている範囲だけで
最大値と最小値を考える
