点Oを極とする極座標表示で表された曲線上の点をPとするとき,線分OPの通過領域の面積を求める際に,強力な威力を発揮するのが扇型分割による積分です.ここではこの積分公式の証明を行います.
高校数学[総目次]
高校数学ワンポイント
| |
スライド |
ノート |
| 1. ファクシミリの原理 |
|
|
| 2. バウムクーヘン分割 |
|
|
| 3. 円と放物線 |
|
|
| 4. 垂線の長さ |
|
|
| 5. 不定方程式 |
|
|
| 6. 関数の連続性は導関数に遺伝するか |
|
|
| 7. 極方程式における r の正負について |
|
|
| 8. 極座標表示における扇形分割積分 |
|
|
| 9. 素因数分解の一意性 |
|
|
| 10. 三角関数の不定積分 |
|
|
| 11. コーシー・シュワルツの不等式 |
|
|
| 12. 放物線と2接線で囲まれた部分の面積 |
|
|
| 13. 整式の除法(発展編) |
|
|
| 14. 3次関数のグラフの特徴 |
|
|
| 15. 曲線の長さを求める公式の証明について |
|
|
| 16. もう迷わない!必要条件・十分条件のくすっと笑える判定方法 |
|
|
| 17. 同じものを含む円順列の考え方 |
|
|
| 18. f(f(x))=x の形をした関数方程式の取り扱い方 |
|
|
| 19. パラメータが2次で表された直線の通過領域 |
|
|
| 20. 四面体の面上及び内部を表すベクトル |
|
|
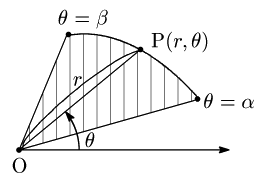
1.扇形分割の積分公式
極座標において,O を極,P
(r,θ) とする.
θ=α から
θ=β まで線分OP が通過する面積は,
∫βα12r2dθ
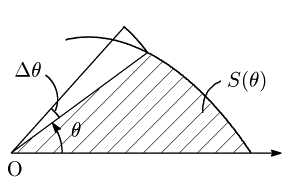
証明
図の斜線部分の面積を S(θ) とします.θ が微小量 Δθ(>0) だけ変化したときの面積の変化量は,θ から θ+Δθ までの r の最大値,最小値をそれぞれ M,m とすると
12m2Δθ≦S(θ+Δθ)−S(θ)≦12M2Δθ.
となります.正の数 Δθ で各辺を割ると
12m2≦S(θ+Δθ)−S(θ)Δθ≦12M2.
ここで Δθ→+0 とすると,M→r, m→r となりますから,はさみうちの原理により
(中辺) →12r2 (Δθ→+0)
となります.Δθ<0のときも同様ですから結局
(中辺) →12r2 (Δθ→0)
です.ところで,中辺において Δθ→0とした式
limθ→0S(θ+Δθ)−S(θ)Δθ
は,S′(θ) の定義式に他なりません.つまり,
S′(θ)=12r2
であることがわかりました.従って求める面積は,
S(β)−S(α)=[S(θ)]βα=∫βαS′(θ)dθ=∫βα12r2dθ.
■
2.応用例
扇形分割の積分公式を使って面積を求めてみましょう.この公式が使えるケースは
- 極方程式として r=f(θ) が与えられている場合
- 点(x,y) が r=f(θ) として (x,y)=(rcosθ,rsinθ) と書ける,即ち(xy)=f(θ)(cosθsinθ) と極座標表示できる場合
です.
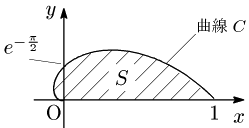
Q. xy 平面上の曲線
C:x=e−θcosθ, y=e−θsinθ (0≦θ≦π) と
x 軸とで囲まれる部分の面積
S を求めよ.
解法の指針
f(θ)=e−θ として,(xy)=f(θ)(cosθsinθ) と表すことができますから,扇形分割の積分公式が使えます.
答
r2=e−2θ(cos2θ+sin2θ)=e−2θ
となりますから,
S=∫π012e−2θdθ=[−14e−2θ]π0=1−e−2π4 ⋯(答)
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
高校数学ワンポイント
| |
スライド |
ノート |
| 1. ファクシミリの原理 |
|
|
| 2. バウムクーヘン分割 |
|
|
| 3. 円と放物線 |
|
|
| 4. 垂線の長さ |
|
|
| 5. 不定方程式 |
|
|
| 6. 関数の連続性は導関数に遺伝するか |
|
|
| 7. 極方程式における r の正負について |
|
|
| 8. 極座標表示における扇形分割積分 |
|
|
| 9. 素因数分解の一意性 |
|
|
| 10. 三角関数の不定積分 |
|
|
| 11. コーシー・シュワルツの不等式 |
|
|
| 12. 放物線と2接線で囲まれた部分の面積 |
|
|
| 13. 整式の除法(発展編) |
|
|
| 14. 3次関数のグラフの特徴 |
|
|
| 15. 曲線の長さを求める公式の証明について |
|
|
| 16. もう迷わない!必要条件・十分条件のくすっと笑える判定方法 |
|
|
| 17. 同じものを含む円順列の考え方 |
|
|
| 18. f(f(x))=x の形をした関数方程式の取り扱い方 |
|
|
| 19. パラメータが2次で表された直線の通過領域 |
|
|
| 20. 四面体の面上及び内部を表すベクトル |
|
|