高校数学[総目次]
数学A 第1章 場合の数
| スライド | ノート | 問題 | |
| 1. 集合 | |||
| 2. 場合の数 | |||
| 3. 順列 | |||
| 4. 円順列・重複順列 | |||
| 5. 組合せ | |||
| 6. 二項定理 |

演習問題
問題1【基本】
1, 2, 3 の3枚のカードから1枚ずつ順に取り出して2桁の整数を作るとき,できる整数は何通りあるか.また,その全てを書き出しなさい.
問題2【基本】
1から6までの目が出るサイコロを1回投げるとき,
A:2以下の目が出る場合
B:5以上の目が出る場合
AまたはBが出る場合は何通りあるか.
問題3【基本】
1から6までの目が出るサイコロを1回投げるとき,
A:2以下の目が出る場合
B:偶数の目が出る場合
AまたはBが出る場合は何通りあるか.
問題4【基本】
赤玉・白玉・青玉が1個ずつ入った袋から1個玉を取り出し,さらに1から3まで書かれたカードを1枚引くとき,玉とカードの組み合わせは全部で何通りあるか.
問題5【基本】
大小2つのサイコロを同時に1回投げるとき,大のサイコロは3以下,小のサイコロは偶数の目が出る場合は何通りあるか.

樹形図で書き出すことで「漏れなく・ダブりなく」数えられます.
解答
1枚目に1,2,3のいずれかを選び,2枚目に残った2枚から1枚を選ぶ.これを樹形図で確かめると,できる2桁の整数は12, 13, 21, 23, 31, 32 の6通りとなります.
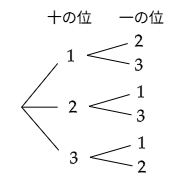
答えは 12, 13, 21, 23, 31, 32の6通り
「同時に起こらない」場合の和の法則です.
解答
A:1,2 の2通り
B:5,6 の2通り
AとBは重なりがないので,和の法則より 2+2=4 通り.
答えは 4通り
重なりがある場合は「AまたはB=(Aの場合の数)+(Bの場合の数)-(AかつBの場合の数)」となります.
解答
A:1,2 の2通り
B:2,4,6 の3通り
AとBの重なりは「2」だけなので,
2+3−1=4 通り(1,2,4,6)
答えは 4通り
それぞれの玉に対してカードが3通りずつあるので,積の法則が使えます.
解答
玉の選び方:3通り
カードの選び方:3通り
積の法則より 3×3=9 通り
答えは 9通り
大のサイコロがどの目でも,小のサイコロは3通りずつあるので,ここでも積の法則が使えます.
解答
大のサイコロが3以下:1,2,3 の3通り
小のサイコロが偶数:2,4,6 の3通り
積の法則より 3×3=9 通り
答えは 9通り
