数学A　場合の数
4．円順列・重複順列【演習問題】

数学A　第1章　場合の数

	スライド	ノート	問題
1. 集合
2. 場合の数
3. 順列
4. 円順列・重複順列
5. 組合せ
6. 二項定理

演習問題

問題１【基本】
5人が丸テーブルを囲んで座るとき，座り方は何通りあるか．

問題２【基本】
赤玉2個と青玉2個を円形に並べる方法は何通りあるか．ただし，同じ色の玉は区別しない．

問題３【基本】
6個の異なるビーズを使ってネックレスを作るとき，できるネックレスの作り方は何通りあるか．

問題４【基本】
0, 1, 2 の3つの数字を使って，重複を許して3桁の整数を作るとき，何通りできるか．

問題５【基本】
1, 2, 3 の3つの数字を使い，重複を許して4桁の整数を作る．ただし，同じ数字が隣り合ってはならない．このとき何通りの整数を作ることができるか．

問題１【基本】

5人が丸テーブルを囲んで座るとき，座り方は何通りあるか．

円順列では「誰か1人を固定」して，残りを並べる順列を考えます．

解答

円順列の公式 $(n-1)!$ において， $n=5$ なので， $(5-1)!=4!=24$ (通り)．

答えは　24通り

問題２【基本】

赤玉2個と青玉2個を円形に並べる方法は何通りあるか．ただし，同じ色の玉は区別しない．

同じものを含む円順列は，一般には難しくなりますが，本問のようなケースまでならすべてを書き出すことで何とかなります．

解答

円形に並べたときに，異なるものは
　赤赤青青　と　赤青赤青
の2通りです．

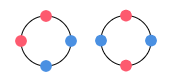
答えは　2通り

補足

同じものを含む順列が大学入試で出題されると，難問化する傾向にあります．詳しくは，高校数学ワンポイント同じものを含む円順列の考え方 を参照してください。

問題３【基本】

6個の異なるビーズを使ってネックレスを作るとき，できるネックレスの作り方は何通りあるか．

ネックレスは回転だけでなく，裏返し（反転）も同じとみなすため，円順列の半分になります．

解答

数珠順列の公式 $\dfrac{(n-1)!}{2}$ において， $n=6$ なので， $\dfrac{5!}{2} = \dfrac{120}{2} = 60$ (通り)．

答えは　60通り

問題４【基本】

0, 1, 2 の3つの数字を使って，重複を許して3桁の整数を作るとき，何通りできるか．

同じものを複数回選ぶことは許されますが，最高位である百の位に0を持ってくることはできません．

解答

百の位は1か2の2通り．
どちらの場合であっても，十の位と一の位は0，1，2の3通りがあるから，十の位と一の位の決め方は， $3^2=9$ (通り)
よって題意の3桁の数は　2×9＝18(通り)

答えは　18通り

問題５【基本】

1, 2, 3 の3つの数字を使い，重複を許して4桁の整数を作る．ただし，同じ数字が隣り合ってはならない．このとき何通りの整数を作ることができるか．

最初の桁は何でもOK，2桁目以降は前と違う数字を選ぶという積の法則です．

解答

まず，1桁目は3通り．
2桁目以降は，前の桁と同じ数字は選べないので2通りずつ．
したがって， $3 \times 2 \times 2 \times 2 = 24$ (通り)．