高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | ||
| 4. 三角関数の導関数 | |||
| 5. 対数関数・指数関数の導関数 | |||
| 6. 媒介変数表示と導関数 | |||
| 7. 陰関数の導関数 | |||
| 8. 平均値の定理 | |||
| 9. 関数の値の変化 | |||
| 10. 関数の極大・極小 | |||
| 11. 関数のグラフ |

1.微分係数と導関数
1.1 微分係数
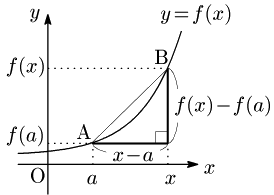
$a$ を固定し,$x\to a$ としたとき,平均変化率 $\dfrac{f(x)-f(a)}{x-a}\cdots$① が極限値をもつとき,$f(x)$ は $x=a$ で微分可能であるという.また,①を $f'(a)$ で表す:
\[ f'(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}\]
補足
上の $x$ の代わりに $a+h$ とすれば,
\[\frac{f(x)-f(a)}{x–a}=\frac{f(a+h)-f(a)}h\]
と書くことができる.(分母が $h$ だけの方が,約分に気付きやすいことがある.)
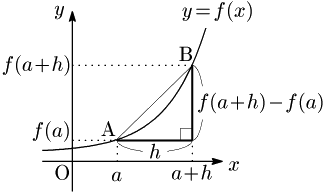
\[ f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}h \]
例題 $f(x)=x^3$ のとき,$f'(1)$ を求めよ.
その1
\[\begin{align*}
f'(1)&=\lim_{x\to
1}\frac{x^3-1}{x-1}\\[5pt]
&=\lim_{x\to 1}\frac{(x-1)(x^2+x+1)}{x-1}\\[5pt]
&=\lim_{x\to1}(x^2+x+1)\\[5pt]
&=3
\end{align*}\]
その2
\[\begin{align*}
f'(1)&=\lim_{h\to
0}\frac{(1+h)^3-1^3}h\\[5pt]
&=\lim_{h\to 0}\frac{h(3+3h+h^2)}h\\[5pt]
&=\lim_{h\to 0}(3+3h+h^2)\\[5pt]
&=3
\end{align*}\]
定理
\[f(x)\mbox{が}x=a\mbox{で微分可能}\Rightarrow f(x)\mbox{は}x=a\mbox{で連続}\]
証明
\[\begin{align*}
\lim_{x\to a}\{f(x)-f(a)\}&=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}\cdot(x-a)\\[5pt]
&=f'(a)\cdot0\\[5pt]
&=0
\end{align*}\]
■
注意
逆 $(\Leftarrow)$ は成り立たない.反例として,$f(x)=|x|$ は $x=0$ で連続だが,$x=0$ で微分可能ではない.

1.2 導関数
関数 $y=f(x)$ がある区間内の任意の $x$ で微分可能であるとき, \[\lim_{h\to 0}\frac{f(x+h)-f(x)}h\] を $f(x)$ の導関数といい, \[f'(x),\ y’\ ,\frac{dy}{dx},\ \frac d{dx}f(x)\] などで表す.また,$f(x)$ の導関数を求めることを「 $f(x)$ を微分する」という.

1.3 導関数の性質
導関数の性質
\begin{align*}&[1]\ \ \{kf(x)\}’=kf'(x)\ \
(k\mbox{は定数})\\\\
&[2]\ \ \{f(x)+g(x)\}’=f'(x)+g'(x)\end{align*}