高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | ||
| 4. 三角関数の導関数 | |||
| 5. 対数関数・指数関数の導関数 | |||
| 6. 媒介変数表示と導関数 | |||
| 7. 陰関数の導関数 | |||
| 8. 平均値の定理 | |||
| 9. 関数の値の変化 | |||
| 10. 関数の極大・極小 | |||
| 11. 関数のグラフ |

11.関数のグラフ
11.1 曲線の凹凸
微分可能な関数のグラフを考える.
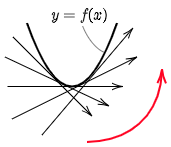
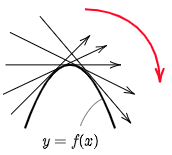
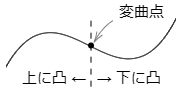
ある区間で,接線の傾きが増加しているとき,グラフはその区間で下に凸という.逆にその区間で接線の傾きが減少しているとき,グラフはその区間で上に凸という.
(接線の傾きが増加)
(接線の傾きが減少)
例えばある区間で,$f'(x)$ の導関数である $f^{\prime\prime}(x)$ が常に正ならば,$f'(x)$ は単調に増加するから,$f(x)$ の接線の傾きは増加していく.即ち,その区間でグラフは下に凸である.ある区間で常に $f^{\prime\prime}(x) < 0$ となる場合も同様である.
まとめ 関数 $f(x)$ が $f^{\prime\prime}(x)$ をもつとき,
常に $f^{\prime\prime}(x)\!>\!0$ である区間でグラフは下に凸である.
常に $f^{\prime\prime}(x)<\!0$ である区間でグラフは上に凸である.

11.2 変曲点
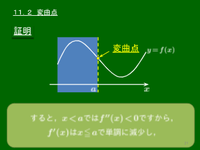
曲線の凹凸の境目を変曲点という.
変曲点であるための必要条件
第2次導関数 $f^{\prime\prime}(x)$ をもつ関数 $f(x)$ について,グラフが $x=a$ を含むある区間において,$x=a$ で上に凸から下に凸に変わるとする.
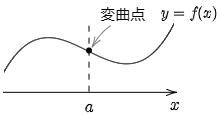
その区間内の $x<a$ で $f^{\prime\prime}(x) < 0$,$x > a$ で $f^{\prime\prime}(x) > 0$ だから,$f^{\prime\prime}(x)$ が連続ならば $f^{\prime\prime}(a)=0$
$x=a$ で下に凸から上に凸に変わる場合も,同様の理由で $f^{\prime\prime}(a)=0$ となる.
定理 関数 $f(x)$ の第2次導関数 $f^{\prime\prime}(x)$ が連続のとき,
\[ \mbox{点}(a,\ f(a))\mbox{が変曲点}\ \ \Longrightarrow \ f^{\prime\prime}(a)=0 \]
注意
逆 $(\Leftarrow)$ はいえない.
(反例)
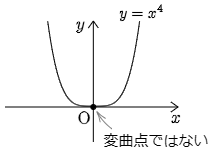
$f(x)=x^4$ について,$f'(x)=4x^3$,$f^{\prime\prime}(x)=12x^2$ であるから,$f^{\prime\prime}(0)=0$.しかし,点$(0,f(0))$ は変曲点ではない.

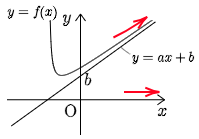
11.3 漸近線の求め方
関数 $y=f(x)$ のグラフにおいて,
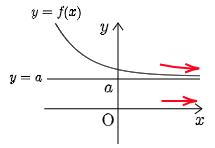
① $\displaystyle\lim_{x\to\infty}f(x)=a$,または$\displaystyle\lim_{x\to-\infty}f(x)=a$
→ 直線 $y=a$ は漸近線.
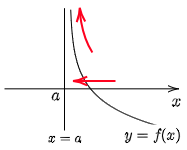
② $\displaystyle\lim_{x\to a+0}f(x)=\infty$,又は$\displaystyle\lim_{x\to a+0}f(x)=-\infty$
又は$\displaystyle\lim_{x\to a-0}f(x)=\infty$,又は$\displaystyle\lim_{x\to a-0}f(x)=-\infty$
→ 直線 $x=a$ は漸近線.
③ $\displaystyle\lim_{x\to\infty}\{f(x)-(ax+b)\}=0$,又は$\displaystyle\lim_{x\to-\infty}\{f(x)-(ax+b)\}=0$
→ 直線 $y=ax+b$ は漸近線.