高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | ||
| 4. 三角関数の導関数 | |||
| 5. 対数関数・指数関数の導関数 | |||
| 6. 媒介変数表示と導関数 | |||
| 7. 陰関数の導関数 | |||
| 8. 平均値の定理 | |||
| 9. 関数の値の変化 | |||
| 10. 関数の極大・極小 | |||
| 11. 関数のグラフ |

2.合成関数の導関数
2.1 合成関数
微分が劇的にラクになる!?
例として4次関数 $y=(x^2-2x)^2-3(x^2-2x)+4$ を取り上げることにしよう.
この関数は大した計算もなしに $x=1$ のとき $y’=0$ であることがわかる.実際,展開してみれば,
\[\begin{align*}
y&=(x^4-4x^3+4x^2)-3(x^2-2x)+4\\[5pt]
&=x^4-4x^3+x^2+6x+4
\end{align*}\]
となる.従って,
\[\begin{align*}
y’&=4x^3-12x^2+2x+6\\[5pt]
&=2(2x^3-6x^2+x+3)\\[5pt]
&=2(x-1)(2x^2-4x-3)
\end{align*}\]
である.ここで $x=1$ を代入すれば $y’=0$ であることは,もはや疑いようもない.
だが,こうした手続きの1つ1つを「大した計算もなしに」と呼ぶのはいささか違和感がある.むしろ,相応の手間がかかると言った方が,より事実に即しているだろう.
従って「大した計算もなしに」という言葉が指し示すものは,当然ながら上記のような展開や整理とは異なる,まったく別種の計算方法である.
その方法によれば,先ほどの煩雑な操作を経ることなく,遥かに洗練された手順で微分を済ませることができるのだ.
その詳細については,次節以降で改めて論じることとし,ここではその導入部分のみを述べておきたい.
冒頭の4次関数 $y=(x^2-2x)^2-3(x^2-2x)+4$ には,$x^2-2x$ という,いかにも意味ありげな塊が2度現れる.これを $f(x)$ と名付けてみる.すると,元の関数は
\[y=\{f(x)\}^2-3f(x)+3\]
という,いわば「関数の中の関数」として再構成される.
このような「ミックス」の構造を持つ関数に対しては,私たちが今まさに学ぼうとする微分の公式が,まるで精巧な機械仕掛けのように,静かに,しかし確実に作動するのである.その仕掛けこそが,計算を大幅に省力化する源泉となる.「大した計算もなしに」$y’=0$ がわかるのは,まさにこの仕掛けによるものなのである.
合成関数とは何か
「ミックス」の構造を持つ関数について,もう少し卑近な例を出そう.
あるスーパーで $x$ 円の商品を手に取り,レジに向かうとする.
すると,消費税10%という,財布の中身に対して容赦なく加算される率が待ち受けており,支払うべき金額 $y$ は $y=1.1x$ となる.この右辺を $f(x)$ とする.すなわち $f(x)=1.1x$ である.
次に,物価高にあえぐ家計の,せめてもの慰めとでも呼ぶべきか,税込金額の2倍のポイントが付与されるという,まるで値上げの荒波の中にひっそりと咲く一輪の花のような制度が控えているとする.このポイント数を $z$ とすると $z=2y$ である.これを $g(y)$ とすると,$g(y)=2y$ である:
\[\left\{\begin{array}{l}y=f(x)=1.1x\\[5pt]z=g(y)=2y\end{array}\right.\]
このように $x$ 円の買い物をしたあとに得られるポイント数を計算するには
$x$ から $y=f(x)$ へ,そして $y$ から $z=g(y)$ へ
と2つのステップを経て求められる.しかし今
\[z=g(y)=g(f(x))=2f(x)=2.2x\]
としてしまえば,途中の $y$ を経由せず,$x$ から $z$ を直接計算できる.
上の $g(f(x))$ のように,2つの関数をミックスさせた関数は,次に説明する合成関数と呼ばれている.
合成関数 $x$ を1つ決めると $f(x)$ がただ1つ決まり,その $f(x)$ に応じて $g(f(x))$ がただ1つ定まるとき,$g(f(x))$ を $f(x)$ と $g(x)$ の合成関数といい,$(g\circ f)(x)$ で表す.
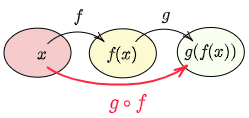
関数が合成関数 $(g\circ f)(x)=g(f(x))$
注意
① $g(x)$ の $x$ のところに $f(x)$ が入るから,$f(x)$ の値域が $g(x)$ の定義域に含まれていなければならない.
例 $f(x)=x-1,\ g(x)=\sqrt x$ のとき,
$(g\circ f)(x)=g(f(x))=\sqrt{x-1}\ \cdots
(*) $
よって $f(x)$ の値域が0以上 $(x\geqq1)$ のとき,$(*)$ は意味を持つ.

