高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | ||
| 4. 三角関数の導関数 | |||
| 5. 対数関数・指数関数の導関数 | |||
| 6. 媒介変数表示と導関数 | |||
| 7. 陰関数の導関数 | |||
| 8. 平均値の定理 | |||
| 9. 関数の値の変化 | |||
| 10. 関数の極大・極小 | |||
| 11. 関数のグラフ |

3.逆関数の微分法
3.1 逆関数とは
まずは関数の復習から
逆関数を論じる前に,「逆」の文字のない通常の「関数」とは何であったかを確認しておこう.
「$\boldsymbol y$ は $\boldsymbol x$ の関数である」とは$x$ の値に対して $y$ の値がただ1つ決まるとき, $\boldsymbol{y}$ は $\boldsymbol{x}$ の関数であるという
例として $y=x+1$ を考える.この式から,
$x=0$ のとき,$y=1$
$x=1$ のとき,$y=2$
$x=2$ のとき,$y=3$
$\vdots$
のように,$x$ の値に対して $y$ の値がただ1つ対応しているから $y$ は $x$ の関数であるといえる.
次に逆の対応を考える
先ほどは,$x$ を先に決めて,その値に応じて $y$ がただ1つの値として導かれた.しかし,今度は思い切ってその順序を反転させ,$y$ の側からこの関係を見つめ直してみる.
$y=1$ のとき,$x=0$
$y=2$ のとき,$x=1$
$y=3$ のとき,$x=2$
$\vdots$
この規則的な連なりは,$x$ が $y$ から1だけ減じた値として,例外なく唯一つ定まることを示している.換言すれば,$x$ は $y$ の関数となっており,最初とは逆の対応関係をなしているのである.
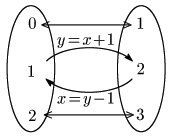
こうして現れた逆方向の対応関係は $x=y-1$ という式で表される.数学においてはしばしば先に決める方の文字を $x$,それに伴って決まる方の文字を $y$ とおくので,この逆対応を表す関数は $x$ と $y$ の文字を入れ替えて
\[x=y-1\ \ \to\ \ y=x-1\]
と表される.この関数 $y=x-1$ をもとの関数 $y=x+1$ の逆関数(inverse function)という.
逆関数とは 関数 $y=f(x)$ について,$y$ の値を先に決めたときにもそれに応じて $x$ の値がただ1つ決まるとする.このとき,$x$ と $y$ を入れ替えた式 $x=f(y)$ を $y$ について解いたときの $x$ の式を関数 $f(x)$ の逆関数といい,$f^{-1}(x)$ で表す.
「$f^{-1}(x)$」は「$f$ インバース $x$」と読まれることが多い.
上の例では $f(x)=x+1$ とすると,$f^{-1}(x)=x-1$ である.
例
関数 $y=2x$ の逆関数
$x=2y$ を $y$ について解いた $y=\dfrac12x$
関数 $y=e^x$ の逆関数
$x=e^y$ を $y$ について解いた $y=\log x$