高校数学[総目次]
数学Ⅱ 第3章 図形と方程式
| スライド | ノート | 問題 | |
| 1. 座標平面上の点 | |||
| 2. 直線の方程式 | |||
| 3. 円の方程式 | |||
| 4. 円と直線 | |||
| 5. 軌跡と方程式 | |||
| 6. 不等式と領域 |

2.直線の方程式
2.1 直線の方程式
[1] 傾き $m$,$y$ 切片 $n$ の直線
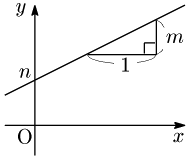
\[y=mx+n\]
[2] 点A$(x_1,y_1)$ を通り,傾き $m$ の直線
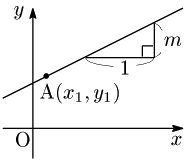
求める直線 :$y=mx+n\ \ \cdots$ ①
これがAを通る:$y_1=mx_1+n\ \ \cdots$ ②
① – ②より,$y-y_1=m(x-x_1)$
\[y-y_1=m(x-x_1)\]
検証
$(x,y)=(x_1,y_1)$ は確かにこの式を満たす.また,この式を変形すると,
\[y=mx-mx_1+y_1\]
となり,$m$ と $-mx_1+y_1$ はともに定数であるから直線を表す.
[3] 2点A$(x_1,y_1)$,B$(x_2,y_2)$ を通る直線
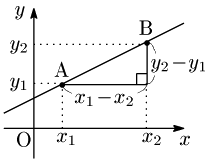
$\underline{1^\circ\ \ x_1\neq x_2 \mbox{のとき}}$
傾き:$\dfrac{y_2-y_1}{x_2-x_1}$
よって [2] より,
\[y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\ \ \cdots(*)\]
補足
2点 A, B の位置関係は,次のいずれであっても上の式で表される.
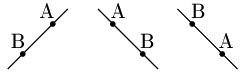
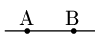
また,$y_1=y_2$ のとき,直線は $x$ 軸に平行になるが,この場合も上の式で表すことができて,
\[y=y_1\]
$\underline{2^\circ\ \ x_1= x_2 \mbox{のとき}}$
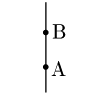
直線は $x$ 軸に垂直であり,$(*)$ の式で表すことができない.このとき直線の方程式は,
\[x=x_1\]
まとめ
傾き $m$,$y$ 切片 $n$ の直線:\[y=mx+n\]
点$(x_1,y_1)$を通り,傾き$m$ の直線:\[y-y_1=m(x-x_1)\]
2点$(x_1,y_1),\ (x_2,y_2)$ を通る直線:
\[\begin{align*}
&x_1\neq x_2 \mbox{ のとき,}y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\\[5pt]
&x_1=x_2 \mbox{ のとき,}x=x_1
\end{align*}\]
補足
例えば $x=2$ とだけ書いたとき,それが
①変数 $x$ の値が2である
②直線 $x=2$ である
のどちらであるかは見た目から区別ができない.もっと言えば平面 $x=2$ とも区別がつかない.この点を明確にするには「直線 $x=2$ 」のように,式の前に図形の名前を明示すればよい.
例題 2点 $(1,1),\ (3,5)$ を通る直線の方程式を求めよ.
答
\[y-1=\frac{5-1}{3-1}(x-1)\ \ \therefore \underline{\boldsymbol{y=2x-1}}\]
別解
\[y-5=\frac{5-1}{3-1}(x-3)\ \ \therefore \underline{\boldsymbol{y=2x-1}}\]
補足
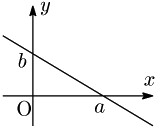
$a\neq0,b\neq0$ とする.2点 $(a,0)$,$(0,b)$ を通る直線の方程式は,
\[y=-\frac bax+b\]
\[\therefore \frac bax+y=b\]
両辺を $b$ で割って次を得る:
\[\frac xa+\frac yb=1\]
例題 2点 $(3,0),\ (0,2)$ を通る直線を求めよ.
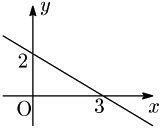
答
\[\underline{\boldsymbol{\frac x3\!+\!\frac y2\!=\!1}}\ \left(y\!=\!-\frac 23 x\!+\!2\right)\]
直線の方程式の一般形
一般に,$x$ と $y$ の1次方程式
$ax+by+c=0\ \ \ \cdots$ ①
(ただし,$a\neq0$ または $b\neq0$)
のグラフは直線である.
逆に,直線の方程式はすべて①の形で表すことができる.

2.2 2直線の関係
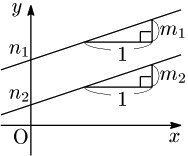
[1] 平行条件
2直線 $y\!=\!m_1x\!+\!n_1\cdots$①,$y\!=\!m_2x\!+\!n_2\cdots$②について,\[\mbox{①}//\mbox{②}\iff m_1=m_2\]
例題 点 $(1,4)$ を通り,直線 $y=-2x+1$ に平行な直線を求めよ.
答 傾きが $-2$ で,点 $(1,4)$ を通る直線だから,
\[\begin{align*}
y-4&=-2(x-1)\\[5pt]
\therefore y&=-2x+6
\end{align*}\]
[2] 垂直条件
2直線 $y\!=\!m_1x\!+\!n_1\cdots$①,$y\!=\!m_2x\!+\!n_2\cdots$②について,\[\mbox{①}\perp\mbox{②}\iff m_1m_2=-1\]
証明
2直線①,②にそれぞれ平行な直線
$y=m_1x\ \ \cdots$ ①$’$,$y=m_2x\ \ \cdots$ ②$’$
が垂直に交わる場合を考えれば十分.
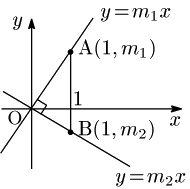
2直線①$’$,②$’$上で,$x$ 座標が1である点をそれぞれA,Bとすると,
\[\begin{align*}
&\mbox{①}’\perp\mbox{②}’\\[5pt]
\iff &\angle{\rm AOB}=90^\circ\\[5pt]
\iff &{\rm OA}^2+{\rm OB}^2={\rm AB}^2\ (\because\mbox{三平方の定理及びその逆})\\[5pt]
\iff &(1^2\!+\!{m_1}^2)\!+\!(1^2\!+\!{m_2}^2)\!=\!(m_1\!-\!m_2)^2\\[5pt]
\iff &m_1m_2=-1
\end{align*}\]
■
例題 直線 $y=2x+5$に垂直な直線の傾きを求めよ.
答
求める直線の傾きを $m$ とすると,
\[2\times m=-1\ \therefore \underline{\boldsymbol{m=-\frac12}}\]
発展的補足
2直線 $a_1x+b_1y+c_1=0\cdots$①,$a_2x+b_2y+c_2=0\cdots$②について,\[\begin{align*}\mbox{①}//\mbox{②}&\iff a_1b_2-a_2b_1=0\\
\mbox{①}\perp\mbox{②}&\iff a_1a_2+b_1b_2=0\end{align*}\]
証明
$b_1\neq0$ かつ $b_2\neq0$ の場合を示す.
①より $y=-\dfrac{a_1}{b_1}x-\dfrac{c_1}{b_1}$
②より $y=-\dfrac{a_2}{b_2}x-\dfrac{c_2}{b_2}$
よって,
\[\begin{align*}
\mbox{①}//\mbox{②}&\iff -\frac{a_1}{b_1}=-\frac{a_2}{b_2}\\[5pt]
&\iff a_1b_2-a_2b_1=0\\[5pt]
\mbox{①}\perp\mbox{②}&\iff -\frac{a_1}{b_1}\cdot\left(-\frac{a_2}{b_2}\right)=-1\\[5pt]
&\iff a_1a_2+b_1b_2=0
\end{align*}\]
■
※ 上の関係は,$b_1=0$ または $b_2=0$ のケースも含めて,ベクトルの内積を用いて示すのが簡潔.
[3] 一致条件
2直線 $a_1x+b_1y+c_1=0$,$a_2x+b_2y+c_2=0$ が一致する条件は,
\[\frac{a_2}{a_1}=\frac{b_2}{b_1}=\frac{c_2}{c_1}\]
ただし,分子か分母の一方でも0のときは,他方も0.
注意
一致条件は,$a_1=a_2$,$b_1=b_2$,$c_1=c_2$ ではない.
例えば,$x+2y+3=0$ と $2x+4y+6=0$ は同じ直線を表す.

2.3 直線に関して対称な点
2点A,Bが,ある点に関して対称というのを既に学んだが,次にこれら2点が,ある直線に関して対称であるという状況を見ていこう.
2点A,Bがある直線 $l$ に関して対称というのは次の図のような状況を指す:
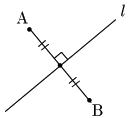
2点A,Bが直線 $l$ に関して対称
$\iff$ (直線AB) $\perp l$ かつ 線分ABの中点が $l$ 上
要するに2点A,Bが,対称の軸である直線 $l$ に関して対称の位置にあるということで,上の図を紙に写し取ったのちに直線 $l$ を折り線として折ると,AとBがぴったり重なるという状況である.
例題 直線 $l:y\!=\!2x\!-\!1$ に関して,点A$(0,4)$ と対称な点B$(p,q)$ を求めよ.
方針
直線に関する対称の定義にある2つの条件,即ち
① $l$⊥(直線AB) ② 線分ABの中点が $l$上
からBの座標を決定する.
答
$\underline{\boldsymbol{l\perp {\rm AB} :}}$
傾きの積が $-1$ より
$2\cdot\dfrac{q-4}{p-0}=-1\ \ \therefore p+2q=8\ \ \cdots$ ①
線分ABの中点が $l$ 上:
線分ABの中点の座標は $\left(\dfrac{0+p}2,\ \dfrac{4+q}2\right)$ であるから
$\dfrac{4+q}2=2\cdot\dfrac{0+p}2-1\ \ \therefore 2p-q=6\ \cdots$ ②
①,②より,$p=4,\ q=2$.
よって,$\underline{\boldsymbol{{\rm B}(4,\ 2)}}$

2.4 2直線の交点を通る直線
例題 $k$ を定数として, \[k(x\!-\!y\!-\!1)\!+\!x\!+\!2y\!-\!4\!=\!0\ \cdots(*)\] はどんな図形を表すか?
こたえ 2直線 $x\!-\!y\!-\!1\!=\!0$, $x\!+\!2y\!-\!4\!=\!0$ の交点を通る直線を表す.
検証
1° 直線を表すことについて
$(*)$を整理すると, \[(k\!+\!1)x\!+\!(-k\!+\!2)y\!+\!(-k\!+\!4)\!=\!0\] これは $a,b,c$ を定数として, \[ax+by+c=0\] の形をしている.
また,$x$ と $y$ の係数は同時には0にならない.
従って,$(*)$は直線を表す.
2° 2直線の交点を通ることについて