例えば四面体の体積を求める際など，空間内の1点から平面に下ろした垂線の長さが必要なことがしばしば起こります．ここでは，垂線の長さの求め方を，空間内の座標が与えられている場合と，そうでない場合について，主にベクトルを用いた考え方についてまとめています．

高校数学[総目次]

高校数学ワンポイント

  スライド ノート
1. ファクシミリの原理    
2. バウムクーヘン分割    
3. 円と放物線    
4. 垂線の長さ    
5. 不定方程式    
6. 関数の連続性は導関数に遺伝するか    
7. 極方程式における $r$ の正負について    
8. 極座標表示における扇形分割積分    
9. 素因数分解の一意性    
10. 三角関数の不定積分    
11. コーシー・シュワルツの不等式    
12. 放物線と2接線で囲まれた部分の面積    
13. 整式の除法(発展編)    
14. 3次関数のグラフの特徴    
15. 曲線の長さを求める公式の証明について    
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法    
17. 同じものを含む円順列の考え方    
18. $f(f(x))=x$ の形をした関数方程式の取り扱い方    
19. パラメータが2次で表された直線の通過領域    
20. 四面体の面上及び内部を表すベクトル    

1．成分が与えられているとき

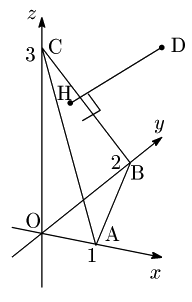
Q.　空間内の 4 点 A$(1,\ 0,\ 0)$，B$(0,\ 2,\ 0)$，C$(0,\ 0,\ 3)$，D$(1,\ 2,\ 3)$ について，点 D から平面 ABC に下ろした垂線の足を H とするとき，DH の長さを求めなさい．

　この問題に対する以下の5つの解法を順に説明します:

  1. $1^\circ$ $\overrightarrow{\mathstrut{\rm{DH}}}=r\overrightarrow {\mathstrut{\rm{DA}}}+s\overrightarrow{\mathstrut{\rm{DB}}}+t\overrightarrow {\mathstrut{\rm{DC}}}$, $r+s+t=1$ とおく．
  2. $2^\circ$ $\overrightarrow {\mathstrut{\rm{DH}}}=\overrightarrow{\mathstrut{\rm{DA}}}+s\overrightarrow {\mathstrut{\rm{AB}}}+t\overrightarrow {\mathstrut{\rm{AC}}}$とおく．
  3. $3^\circ$ 正射影ベクトルの利用．
  4. $4^\circ$ 点 $\rm D$ を通る直線の方程式を利用．
  5. $5^\circ$ 点と平面の距離の公式を利用．

お手軽さの順は，軽い方から概ね
\[3^\circ,\ 5^\circ > 4^\circ \gg 1^\circ,\ 2^\circ\]
です．

$1^\circ$ $\overrightarrow{\mathstrut{\rm{DH}}}\!=
\!r\overrightarrow {\mathstrut{\rm{DA}}}
\!+
\!s\overrightarrow{\mathstrut{\rm{DB}}}
\!+
\!t\overrightarrow {\mathstrut{\rm{DC}}}$ , $r\!+\!s\!+\!t\!=\!1$とおく

　$\overrightarrow{\mathstrut{\rm{DH}}}=r\overrightarrow{\mathstrut{\rm{DA}}}+s\overrightarrow{\mathstrut{\rm{DB}}}+t\overrightarrow{\mathstrut{\rm{DC}}},\ r+s+t=1\cdots①$ とおきます.
　$\overrightarrow{\mathstrut{\rm{DA}}}=(0,-2,-3),\overrightarrow{\mathstrut{\rm{DB}}}=(-1,0,-3),\overrightarrow{\mathstrut{\rm{DC}}}=(-1,-2,0)$ ですから，

\[\begin{align*}
\overrightarrow{\mathstrut{\rm{DH}}}&=r(0,\ -2,\ -3)+s(-1,\ 0,\ -3)+t(-1,\ -2,\ 0)\\[5pt]
&=(-s-t, -2r-2t, -3r-3s)
\end{align*}\]

です．$\overrightarrow{\mathstrut{\rm{DH}}}\perp\overrightarrow{\mathstrut{\rm{AB}}}$ かつ $\overrightarrow{\mathstrut{\rm{DH}}}\perp\overrightarrow{\mathstrut{\rm{AC}}}$
により，

\[\begin{align*}
&(-s-t, -2r-2t, -3r-3s)\cdot(-1,\ 2,\ 0)=0\cdots\mbox{②}\\[5pt]
&(-s-t, -2r-2t, -3r-3s)\cdot(-1,\ 0,\ 3)=0\cdots\mbox{③}
\end{align*}\]

　①～③ より　$r=-\dfrac{23}{49},\ s=\dfrac{31}{49},\ t=\dfrac{41}{49}$．
　従って $\overrightarrow{\mathstrut{\rm{DH}}}=-\dfrac{12}{49}(6,\ 3,\ 2)$ となりますから，

\[{\rm DH}=\left|-\frac{12}{49}\right|\sqrt{6^2+3^2+2^2}=\bf{\frac{12}7} \]

$2^\circ$ $\overrightarrow {\mathstrut{\rm{DH}}}\!=
\!\overrightarrow{\mathstrut{\rm{DA}}}
\!+
\!s\overrightarrow {\mathstrut{\rm{AB}}}
\!+
\!t\overrightarrow {\mathstrut{\rm{AC}}}$ とおく

　$\overrightarrow{\mathstrut{\rm{DH}}}=\overrightarrow{\mathstrut{\rm{DA}}}+s\overrightarrow{\mathstrut{\rm{AB}}}+t\overrightarrow{\mathstrut{\rm{AC}}}$ とおきます．
　$\overrightarrow{\mathstrut{\rm{DA}}}=(0,-2,-3),\ \overrightarrow{\mathstrut{\rm{AB}}}=(-1,2,0),\ \overrightarrow{\mathstrut{\rm{AC}}}=(-1,0,3)$ ですから，
\[\begin{align*}
\overrightarrow{\mathstrut{\rm{DH}}}&=(0,\ -2,\ -3)+s(-1,\ 2,\ 0)+t(-1,\ 0,\ 3)\\[5pt]
&=(-s-t,\ -2+2s,\ -3+3t)
\end{align*}\]
です．　$\overrightarrow{\mathstrut{\rm{DH}}}\perp\overrightarrow{\mathstrut{\rm{AB}}}$ かつ $\overrightarrow{\mathstrut{\rm{DH}}}\perp\overrightarrow{\mathstrut{\rm{AC}}}$ により，
\[\begin{align*}
&(-s-t,\ -2+2s,\ -3+3t)\cdot(-1,\ 2,\ 0)=0\cdots\mbox{①}\\[5pt]
&(-s-t,\ -2+2s,\ -3+3t)\cdot(-1,\ 0,\ 3)=0\cdots\mbox{②}
\end{align*}\]
　①，②より　$s=\dfrac{31}{49},\ t=\dfrac{41}{49}$．
　従って $\overrightarrow{\mathstrut{\rm{DH}}}=-\dfrac{12}{49}(6,\ 3,\ 2)$ となりますから，
\[{\rm DH}=\left|-\frac{12}{49}\right|\sqrt{6^2+3^2+2^2}=\bf{\frac{12}7} \]

補足

　上の解答のようにして $s$ と $t$ を求めておいたのち，$\overrightarrow{\rm{DH}}$ の大きさを求める際には次のようにしてもよいでしょう：

\[\begin{align*}
|\overrightarrow{\rm{DH}}|^2&=\overrightarrow{\rm{DH}}\cdot\overrightarrow{\rm{DH}}\\[5pt]
&=\overrightarrow{\rm{DH}}\cdot\bigl(\overrightarrow{\rm{DA}}+\frac{31}{49}\overrightarrow{\rm{AB}}+\frac{41}{49}\overrightarrow{\rm{AC}}\bigr)\\[5pt]
&=\overrightarrow{\rm{DH}}\cdot\overrightarrow{\rm{DA}}\ \ (\because \overrightarrow{\rm{DH}}\perp\overrightarrow{\rm{AB}},\ \overrightarrow{\rm{DH}}\perp\overrightarrow{\rm{AC}})\\[5pt]
&=-\frac{12}{49}(6,\ 3,\ 2)\cdot(0,\ -2,\ -3)\\[5pt]
&=\frac{12^2}{49}\\[8pt]
\therefore |\overrightarrow{\rm{DH}}|&={\bf \frac{12}7}
\end{align*}\]

　この $\overrightarrow{\rm{DH}}$ の一方だけを残して計算するという方法は，ベクトルの成分が与えられていない場合に極めて有効です．

$3^\circ$ 正射影ベクトルの利用

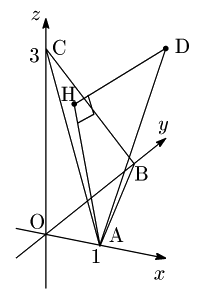
　$\overrightarrow{\mathstrut{\rm{AB}}}$ と $\overrightarrow{\mathstrut{\rm{AC}}}$ の双方に垂直なベクトルの 1 つとして
$\overrightarrow{\mathstrut{n}}=(6,\ 3,\ 2)$ がとれます．実際，

\[\begin{align*}
\overrightarrow{\rm{AB}}\cdot\overrightarrow{\mathstrut{n}}&=(-1,\ 2,\ 0)\cdot(6,\ 3,\ 2)\\[5pt]
&=-6+6+0=0\\[5pt]
\overrightarrow{\rm{AC}}\cdot\overrightarrow{\mathstrut{n}}&=(-1,\ 0,\ 3)\cdot(6,\ 3,\ 2)\\[5pt]
&=-6+0+6=0\\[5pt]
\end{align*}\]

です．$\overrightarrow{\mathstrut{\rm{DH}}}$ は(例えば) $\overrightarrow{\mathstrut{\rm{DA}}}$ の $\overrightarrow{\mathstrut{n}}$ への正射影ベクトルですから，