高校数学[総目次]
高校数学ワンポイント

1. はじめに
平面上の点 P を極座標表示によって (r, θ) と表したときの r は,極 O と点 P との距離であって, r≧ です.
r を r\geqq 0 に制限すると,r と \theta の関係式 r=f(\theta)(極方程式)において,例えば
r=\cos\theta -1\ \cdots \mbox{①}
は,\theta=2n\pi\ (n は整数) のとき r=0 となり,それ以外の \theta では r < 0 となりますから,方程式①は1点 O (極)のみを表す式となります.
ここで,r < 0 となる \theta に対しては,(-r,\ \theta +\pi) なる点に対応させると約束すれば,①は次のような曲線(カージオイド)を表すことになります:
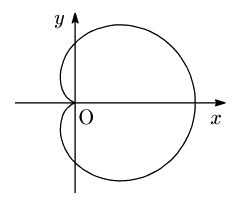
平面上の点に対して2通りの表現を許す,即ち
\mbox{点}(r,\ \theta)=\mbox{点}(-r,\ \theta+\pi)
とすることによって,例えば次のような直交座標系における直線 y=x を極方程式で表すと,
- r\geqq 0 に制限:\theta=\dfrac \pi 4,または \theta=\dfrac 54\pi.
- r < 0 も許す:\theta=\dfrac \pi 4.\ \left(\mbox{または}\ \theta=\dfrac 54\pi.\right)
といった具合に,r<0 も許すと,\theta=\dfrac \pi 4 と \theta=\dfrac 54\pi のどちらか一方を書くだけでよくなり,式を簡単にすることができます.
一方,r < 0 を許したことで,平面上における幾何的な考察をややこしくしている場合があります.
例えば,次のような図において,r>0 のとき,
\mbox{PH}=|a-r\cos\theta |\ \ \cdots \mbox{②}
となることには誰もが疑いをはさまないでしょう.
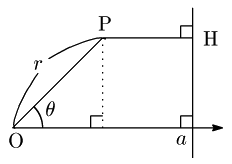
ここで「点 P が曲線 r=\cos\theta -1( \leqq 0) 上を動く」などという状況を考えるとき,PH を \theta の関数として
\mbox{PH}=|a-(\cos\theta-1)\cos\theta|\ \ \cdots ③
と書いて大丈夫なのだろうか?という不安は生じないでしょうか.

2.極方程式における見方の転換
ここでひとまず極座標 (r,\ \theta) における r と \theta が,それぞれ線分の長さと角度であるという幾何的な描像を忘れて,極方程式 r=f(\theta) から得られる r と \theta の組に対して次のような見方をしてみましょう:
r=f(\theta) によって定まる (r,\ \theta) の組は,極 O を原点,始線を x 軸の正の向きとする直交座標の (x,\ y) を
(x,\ y)=(r\cos\theta,\ r\sin\theta)
によって与えるものである.
