高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | ||
| 2. 関数のグラフの移動 | |||
| 3. 2次関数の最大・最小 | |||
| 4. 2次関数の決定 | |||
| 5. 2次関数のグラフと方程式 | |||
| 6. 2次不等式とグラフ | |||
| 7. 2次方程式の解の配置 |

1. 2次関数のグラフ
2次関数は高校数学の根幹をなす
中学校では「$y$ が $x$ の関数で,$y=ax^2(a\neq0)$ の形で表されるとき,$y$ は $x^2$ に比例する」という形で2次関数を教わる.これは私たちにとって大変大きな転換点であった.
2次関数が導入される以前は,例えば「毎分70mで $x$ 分歩けば,その距離はいくらになるのか」といった,ひたすら等間隔に延びる世界——あるいは「水槽に蓄えられた5Lの水が,毎分2Lずつ増していく」という,きわめて素朴な直線的関係——そうした,筋道の見通しが良すぎるほど単純な現象だけが扱われていた.
だが,2次関数という概念の導入は,その直線性に安住していた思考を,全く異なる景色へと導く契機となる.
相似比が $1:x$ の2つの三角形が,面積に話題を移した瞬間に2乗の比を要求しはじめることや,高い場所から物体を放てば,$t$ 秒の移動距離が時間の2乗に比例して増大していくこと──こうした曲線的な事象の背後に潜む規則性を,数学はようやく視界に収めるのである.
こうして私たちは,線形の世界を超えて曲線の領域へと踏み出す.高校の数学Ⅰでは,この拡張された視野をさらに押し広げ,より複雑な,そしてより豊かな形式へと踏み込んでいく.最終形は $y=ax^2+bx+c$ であり,ゴールまでのアウトラインは次のようになる.
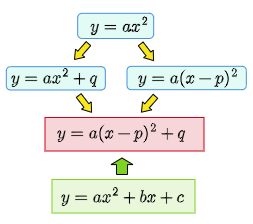
「最終形が $y=ax^2+bx+c$ なら,最後の緑色の矢印は下向きであるべきではないか」——そういぶかる向きもあるだろう.確かに,学習の順序として最後に登場するのはこの $y=ax^2+bx+c$ であり,その意味では“終点”と呼んでも差し支えない.しかし,実際にそのグラフを描こうとする瞬間,私たちは必ずといってよいほど $y=a(x-p)^2+q$ という姿に書き換えることを求められる.つまり,$y=ax^2+bx+c$ は形式上の終着でありながら,視覚的理解のためには再び $y=a(x-p)^2+q$ へと引き戻される——その事情を踏まえて,緑の矢印は上向きにしてあるのだ.
2次関数は高等学校のごく初期に学ぶ分野であるが,その影響力は異様なほど広い.他分野の問題に姿を変えて何度も割り込み,特に最大・最小を問う問題においては,最終的に2次関数の理論へと回収されていく構図が繰り返し現れる.大学入試において最重要視される理由も,まさにそこにある.
2次関数とは,学習の扉を開く最初の段階で姿を現しながら,終盤にいたるまで決して手放すことのできない,数学の根幹そのものなのである.

1.1 $y=ax^2$ のグラフ
(復習) $y=ax^2$ のグラフはどのようなものだったか
中学校で習った関数 $y=ax^2$ の復習から始めよう.まずは $a$ が正の場合と負の場合に大きく分けられる.いくつかの例で,グラフの形状や特徴を確認しよう.
$a>0$ のとき
例題1 次の2次関数のグラフをかけ
① $y=x^2$
② $y=2x^2$
③ $y=\dfrac12x^2$
$x$ の値が $-3$,$-2$,$-1$,$0$,$1$,$2$,$3$ の場合を計算して座標平面上にとり,滑らかに連結することでグラフを描いてみよう.
こたえ
① $y=x^2$

② $y=2x^2$
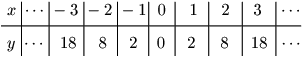
③ $y=\dfrac12x^2$
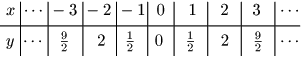
これら3つのグラフは次のようになる:
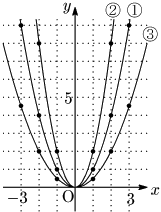
これらのグラフは放物線と呼ばれている.いずれも軸が直線 $x=0$ すなわち $y$ 軸で,グラフと軸との交点である原点 $(0,\ 0)$ を,これらの放物線の頂点という.また,これらのように下にとがった曲線を下に凸(とつ)という.$a$ の値が大きくなるにつれて,グラフがスリムになっていくことが見て取れる.
$a<0$ のとき
例題2 次の2次関数のグラフをかけ
① $y=-x^2$
② $y=-2x^2$
③ $y=-\dfrac12x^2$
$a>0$ の場合と同じように $x$ が整数であるいくつかの値を計算し,グラフを描いてみよう.
こたえ
① $y=-x^2$
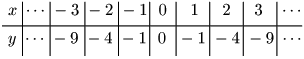
② $y=-2x^2$
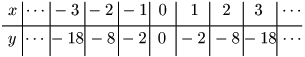
③ $y=-\dfrac12x^2$
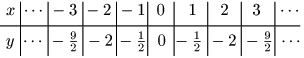
これらのグラフは次のようになる.
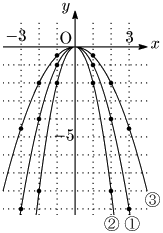
これらのグラフも放物線である.軸が直線 $x=0$ すなわち $y$ 軸であることや,グラフと軸との交点である原点 $(0,\ 0)$ がこれらの放物線の頂点であることも $a>0$ の場合と同様である.大きく異なるのはグラフの形状で,$a>0$ の場合ととがっている向きがが逆になっている.このような曲線を上に凸という.$a$ の値が小さくなるにつれて( $a$ の絶対値が大きくなるにつれて),グラフがスリムになっていくことが見て取れる.
$y=ax^2$ のグラフは $a$ の値によってどう変化するか
$y=ax^2$ の $a$ の値を変化させていったときのグラフの様子を,下のアニメーションで確認しておこう.
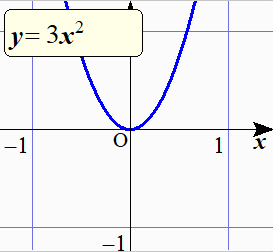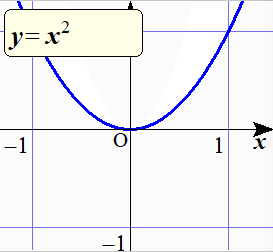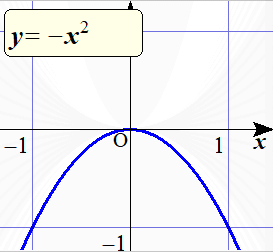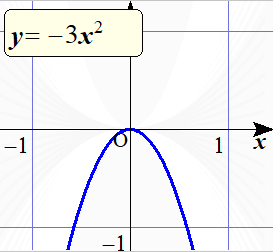
$y=ax^2$ の $a$ の値を
3から-3まで変化させたときの
グラフの変化の様子.
$y=ax^2$ のグラフは $y$ 軸対称
関数 $y=ax^2$ のグラフの特徴の1つとして,$y$ 軸に関して対称であるということが挙げられる.直線 $x=0$ ($y$ 軸) をこの放物線の軸という.また,放物線と軸が交わる点をこの放物線の頂点という.放物線 $y=ax^2$ の頂点は原点 $(0,\ 0)$ である.

1.2 $y=ax^2+q$ のグラフ
$y=ax^2$ に「$+q$」が追加されるとグラフはどうなるか
例 $y=x^2+2$ のグラフは $y=x^2$ のそれと比べてどう違うか.
この関数について,$x$ の値からスタートして $y$ の値が決まる手順は次の通りである:
$x$ $\to$ $x^2$ $\to$ $x^2$+2 $\to$ $y$
$x$ の値が $-2,\ -1,\ 0,\ 1,\ 2$ のときの $y$ の値を調べてみると次のようになる.
| $x$ | $x^2$ | $x^2 \color{red}{+2}$ | $y$ |
|---|---|---|---|
| $-2$ | $4$ | $6$ | $6$ |
| $-1$ | $1$ | $3$ | $3$ |
| $0$ | $0$ | $2$ | $2$ |
| $1$ | $1$ | $3$ | $3$ |
| $2$ | $4$ | $6$ | $6$ |
ここで $y=x^2+2$ と $y=x^2$ の関係を探ってみよう.上の考察から
$y=x^2+2$ の $x=X$ のときの値は, $y=x^2$ の $x=X$ のときの値より2だけ大きい
ことがわかる.これを言い換えると
放物線 $y=x^2+2$ の $x=X$ のときの $y$ 座標は,放物線 $y=x^2$ の $x=X$ のときの $y$ 座標より2だけ大きい
ということがいえる.図で表すと次のようになる:
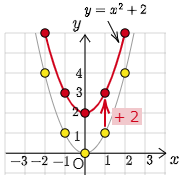
いま,$x$ の値のいくつかについて見てきたが,これを全ての $x$ について隙間なく調べてみると次のようになり,これが $y=x^2+2$ のグラフである.
つまり $y=x^2+2$ のグラフは $y=x^2$ のグラフを $y$ 軸方向に2だけ平行移動したものとなっている.

それでは一般論
一般に,放物線 $y=ax^2\ \ \cdots$ ①上の任意の点を $(x,y)$ とし,この点を $y$ 軸方向に $q$ だけ平行移動した点を $(X,Y)$ とする:
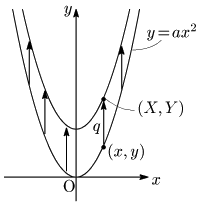
$(x,\ y)$ と $(X,\ Y)$ の関係は,
\[\left\{ \begin{array}{l} X=x\\[5pt] Y=y+q \end{array}\right.\ \ \ \therefore \left\{\begin{array}{l} x=X\\[5pt] y=Y-q \end{array}\right.\]
これらを①に代入すると,$X$ と $Y$ の関係式が得られる:
\[Y-q=aX^2\]
\[\therefore Y=aX^2+q\]
これは点$(X,\ Y)$ が,$y=ax^2+q$ のグラフ上にあることを意味する.
この移動に伴って,2次関数 $y=ax^2+q$ のグラフの頂点は点 $(0,\ q)$ に移動する.一方,グラフの軸は,$y$ 軸のままで,変化しない.
y=ax²+q のグラフ
2次関数 $y=ax^2+q$ のグラフは,$y=ax^2$ のグラフを $y$ 軸方向に $q$ だけ平行移動したものとなる.
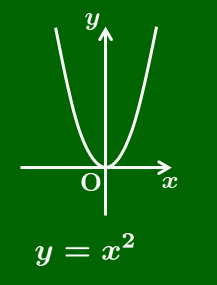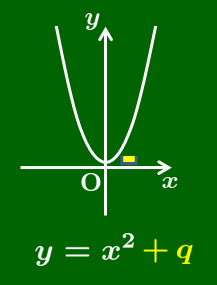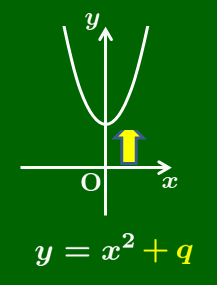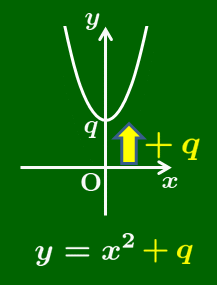
軸は $y$ 軸(直線 $x=0$)
頂点は 点 $(0,\ q)$

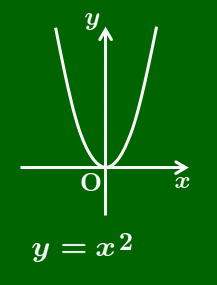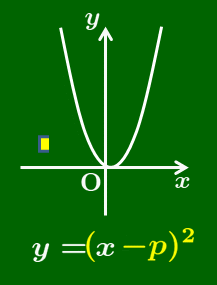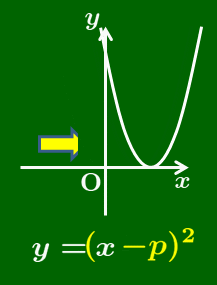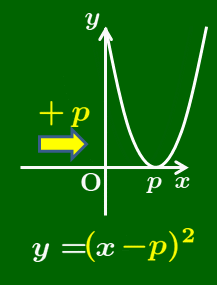
1.3 $y=a(x-p)^2$ のグラフ
$y=ax^2$ の $x$ が $x-p$ に変わるとグラフはどうなるか
例 $y=(x-1)^2$ のグラフは $y=x^2$ のそれと比べてどう違うか.
この関数について,$x$ の値からスタートして $y$ の値が決まる手順は次の通りである:
$x$ $\to$ $x$-1 $\to$ $(x-1)^2$ $\to$ $y$
$x$ の値が $-1,\ 0,\ 1,\ 2,\ 3$ のときの $y$ の値を調べてみると次のようになる.
| $x$ | $x\color{red}{-1}$ | $(x-1)^2$ | $y$ |
|---|---|---|---|
| $-1$ | $-2$ | $4$ | $4$ |
| $0$ | $-1$ | $1$ | $1$ |
| $1$ | $0$ | $0$ | $0$ |
| $2$ | $1$ | $1$ | $1$ |
| $3$ | $2$ | $4$ | $4$ |
ここで $y=(x-1)^2$ と $y=x^2$ の関係を探ってみると,上の具体例の考察から
$x$ のある値 $X$ に対する $(x-1)^2$ の値は, $x $ が $X-1$ のときの $y=x^2$ の値と等しい
ことがわかる.これを言い換えると
放物線 $y=(x-1)^2$ の $x=X$ のときの $y$ 座標は,放物線 $y=x^2$ の $x=X-1$ のときの $y$ 座標と等しい
ということがいえる.図に表すと次のようになる:
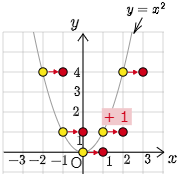
例えば,$y=(x-1)^2$ の $x=2$ のときの $y$ 座標は,$y=x^2$ の $x=1$ のときの $y$ 座標と等しい.
この図を見ると,$x$ の各値に対して「$x-1$」というのは1だけ左側の値を指しており,そこにおける $x^2$ の値が右側へスライドしたものが $y=(x-1)^2$ の $y$ の値であることがわかる.
いま,$x$ の値のいくつかについて見てきたが,これを全ての $x$ について隙間なく調べてみると次のようになり,これが $y=(x-1)^2$ のグラフである.
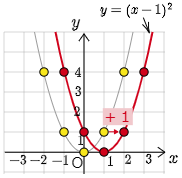
つまり $y=(x-1)^2$ のグラフは $y=x^2$ のグラフを $x$ 軸方向に1だけ平行移動したものとなっているのである.

それでは一般論
放物線 $y=ax^2\ \ \cdots$ ①上の任意の点を $(x,y)$ とし,この点を $x$ 軸方向に $p$ だけ平行移動した点を $(X,Y)$ とする:
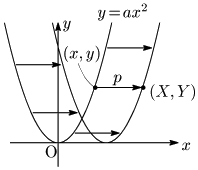
$(x,y)$ と $(X,Y)$ の関係は,
\[\left\{ \begin{array}{l} X=x+p\\[5pt] Y=y \end{array}\right.\ \ \ \therefore \left\{\begin{array}{l} x=X-p\\[5pt] y=Y \end{array}\right.\]
これらを①に代入すると,$X$ と $Y$ の関係式が得られる:
\[Y=a(X-p)^2\]
これは点 $(X,\ Y)$ が $y=a(x-p)^2$ のグラフ上にあることを意味する.
この移動に伴って,2次関数 $y=a(x-p)^2$ のグラフの軸は直線 $x=p$ に移動し,頂点も点 $(p,\ 0)$ に移動する.
y=a(x-p)² のグラフ
2次関数 $y=a(x-p)^2$ のグラフは,$y=ax^2$ のグラフを $x$ 軸方向に $p$ だけ平行移動したものとなる.
軸は 直線 $x=p$
頂点は 点 $(p,\ 0)$

1.4 $y\!=\!a(x\!-\!p)^2\!+\!q$ のグラフ
前2節の変化が両方起こったとき,グラフはどうなるか
1.2節と1.3節で $y$ 軸方向と $x$ 軸方向の平行移動の式を導いたが,それをミックスしたものがこの節で扱う $y=a(x-p)^2+q$ の形で,これが2次関数の変形の最終形となる.
放物線 $y=ax^2\ \ \cdots$ ①上の任意の点を $(x,y)$ とし,この点を
$x$ 軸方向に $p$,$y$ 軸方向に $q$
だけ平行移動した点を $(X,Y)$ とする:
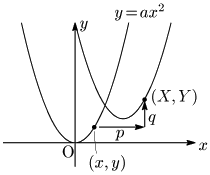
$(x,y)$ と $(X,Y)$ の関係は,
\[\left\{ \begin{array}{l} X=x+p\\[5pt] Y=y+q \end{array}\right.\ \ \ \therefore \left\{\begin{array}{l} x=X-p\\[5pt] y=Y-q \end{array}\right.\]
点 $(x,\ y)$ は放物線①上の点だから代入すると,$X$ と $Y$ の関係式が得られる:
\[Y-q=a(X-p)^2\]
\[\therefore Y=a(X-p)^2+q\ \ (y=a(x-p)^2+q)\]
従って次が成り立つ:
y=a(x-p)²+q のグラフ
2次関数 $y=a(x-p)^2+q$ のグラフは,$y=ax^2$ のグラフを
$x$ 軸方向に $p$,$y$ 軸方向に $q$
だけ平行移動したものとなる.このとき,
軸:直線 $x=p$,頂点 $(p,\ q)$
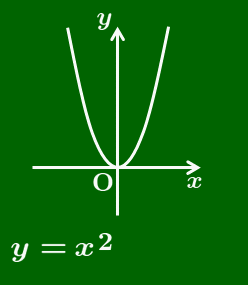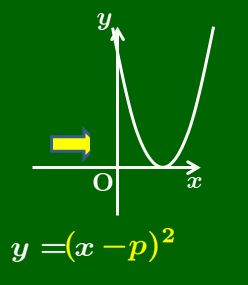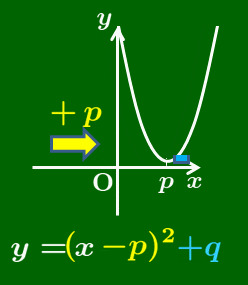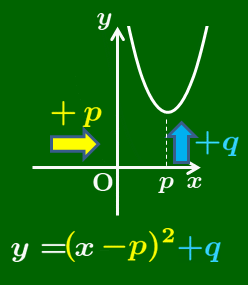

1.5 $y\!=\!ax^2\!+\!bx\!+\!c$ のグラフ
$y=ax^2+bx+c$ は結局 $y=a(x-p)^2+q$ に帰着させる
どのような2次関数も $y=ax^2+bx+c$ の形で表せるが,この形のままだとグラフをかくことは難しい.1.4節で学んだ $y=a(x-p)^2+q$ の形になってこそ,このグラフの状況を詳しくとらえることができるのである.
ポイント 変形して $\boldsymbol{y=a(x-p)^2+q}$ の形にする.
補足
$ax^2+bx+c$ を $a(x-p)^2+q$ の形に変形することを平方完成するという.演習問題 に平方完成のやり方を示したアニメーションを用意した.
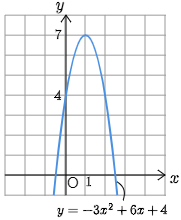
例題 放物線 $y\!=\!-3x^2\!+\!6x\!+\!4$ の軸と頂点の座標を求め,グラフをかけ.
答
解答例を表示するこのあとは演習問題 で理解を確認!

次は,2.関数のグラフの移動
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | ||
| 2. 関数のグラフの移動 | |||
| 3. 2次関数の最大・最小 | |||
| 4. 2次関数の決定 | |||
| 5. 2次関数のグラフと方程式 | |||
| 6. 2次不等式とグラフ | |||
| 7. 2次方程式の解の配置 |