2次関数の最大・最小｜定義域による場合分けと解き方をスライドでやさしく解説

このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

数学Ⅰ　第1章　2次関数

	スライド	ノート	問題
1. 2次関数のグラフ	[無料]
2. 関数のグラフの移動
3. 2次関数の最大・最小
4. 2次関数の決定
5. 2次関数のグラフと方程式
6. 2次不等式とグラフ
7. 2次方程式の解の配置

3.　2次関数の最大・最小

2次関数の最大・最小は，それほど複雑ではない

　2次関数は値が大きくなったり小さくなったりする上，グラフが曲線であるため，1次関数より状況はずっと複雑である．しかし最大・最小を考えるというだけなら，問題となるのは軸を挟んで関数の値が減少から増加に転じたり，その逆に増加から減少に転じたりという点だけである．従って今考えている範囲が軸を含まないなら，1次関数の最大・最小を考えることとさして変わるところはない．

　例えば2次関数 $y = x^{2} - 4 x + 5$ を考えよう．平方完成すると $y = (x - 2)^{2} + 1$ となるから，頂点の座標は $(2, 1)$ ，軸は直線 $x = 2$ である．従ってグラフは次のようになる．

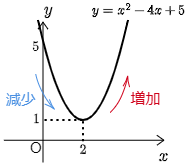
　グラフを見ると

$x ≦ 2$ で減少， $x ≧ 2$ で増加

ということがわかる．よってこの2次関数は $x = 2$ で最小値1をとる．一方， $x$ の値をどんどん小さくしたり，逆にどんどん大きくしていくと， $y$ の値はいくらでも大きくなることもグラフからわかる．従って最大値はない．数学Ⅲになると「 $\infty$ (正の無限大)」という記号が出てきて，これを知っていると「最大値は $\infty$ 」といいたくなるかもしれないがこれは正しくない．数学では「 $\infty$ 」は特定の値を指す記号ではないので最大「値」と呼ぶわけにはいかないのである．
　さてここで，定義域を $3 ≦ x ≦ 4$ に制限してみよう．この範囲における最大値・最小値はどうなっているであろうか．

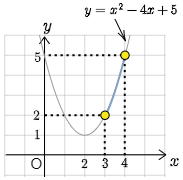
　グラフから一目瞭然， $x = 3$ で最小値2， $x = 4$ で最大値5をとっている．そう判断した私たちの思考を冷静に振り返ってみると，実は1次関数のグラフ，即ち直線を見てどちらがより大きいか小さいかを判断しているときとまるで同じである．途中が曲線だろうが直線だろうが，最大・最小を判断するうえでは問題にならない．グラフが右上がりだということがわかったら，私たちは両端の値しか見ていないのである．

3.1　2次関数の最大・最小

2次関数の最大・最小にはいくつかのパターンがある

　2次関数の最大・最小を考える上で，まず大きく分けて2つの場合がある．一つには定義域に制限がなく実数全体のとき，そしてもう一つには定義域に制限があるときである．後者の場合には更に，軸が含まれるかどうかで場合分けが生じる．

２次関数の最大・最小の大別

定義域に制限がなく実数全体のとき

例題　次の2次関数に最大値，最小値があればそれを求めよ．最大値または最小値をとるときの $x$ の値もあわせて求めよ．
(1) $y = \frac{1}{2} x^{2} + x - 2$
(2) $y = - 2 x^{2} + 2 x + 1$

考え方

　2次関数 $y = a x^{2} + b x + c$ が

$y = a (x - p)^{2} + q$

と変形(平方完成)できたとする．このとき，2次の係数 $a$ が正の場合と負の場合で状況が異なる．

[1]　 $a > 0$ のとき

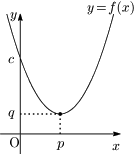
　グラフは図のように下に凸であるから，頂点の $y$ 座標が最小値となるが，最大値の方はいくらでも大きくなるので存在しない．

$x = p$ で最小値 $q$

最大値はない

[2]　 $a < 0$ のとき

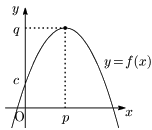
　 $a > 0$ の場合とは逆にグラフは上に凸となるから，頂点の $y$ 座標が最大値となる．一方，最小値の方はいくらでも小さくなるので存在しない．

$x = p$ で最大値 $q$

最小値はない

こたえ

(1) $y = \frac{1}{2} x^{2} + x - 2$ を平方完成すると $\begin{aligned} y & = \frac{1}{2} x^{2} + x - 2 \\ = \frac{1}{2} (x^{2} + 2 x) - 2 \\ = \frac{1}{2} (x + 1)^{2} - \frac{5}{2} \end{aligned}$ 　よって $x = - 1$ で最小値 $- \frac{5}{2}$ をとる．最大値はない．

(2) $y = - 2 x^{2} + 2 x + 1$ を平方完成すると $\begin{aligned} y & = - 2 x^{2} + 2 x + 1 \\ = - 2 (x^{2} - x) + 1 \\ = - 2 {(x^{2} - \frac{1}{2})}^{2} + \frac{3}{2} \end{aligned}$ 　よって $x = \frac{1}{2}$ で最大値 $\frac{3}{2}$ をとる．最小値はない．

問題１【基本】
　次の2次関数に最大値，最小値があればそれを求めよ．最大値または最小値をとるときの $x$ の値もあわせて求めよ．
(1)　 $y = x^{2} - 4 x + 5$ 　(2)　 $y = - 2 x^{2} + 4 x$

答えは 演習問題 へ

定義域に制限があるとき

例題　次の2次関数に最大値，最小値があればそれを求めよ．最大値または最小値をとるときの $x$ の値もあわせて求めよ．
(1) $y = x^{2} - 3 (- 2 ≦ x ≦ 1)$
(2) $y = - 2 x^{2} + 4 x + 1 (0 ≦ x ≦ 3)$
(3) $y = - x^{2} + 4 x (1 < x < 4)$

考え方

　2次関数 $y = a x^{2} + b x + c$ が

$y = a (x - p)^{2} + q$

と変形(平方完成)できたとする．定義域が $x_{1} ≦ x ≦ x_{2}$ のように定義域に制限がかかっているときには，まずもってグラフの軸がその範囲に入っているのかどうかを検討しなければならない．

[1]　軸が定義域に含まれるとき

$a > 0$ のとき

　グラフは下に凸であるから，頂点の $y$ 座標が最小値となる．一方，最大値の方は，グラフが軸に関して対称であることに注意をすると，軸からより遠い方が大きくなり，そこで最大値をとる．

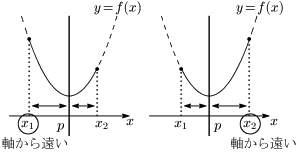
$x = x_{1}$ (or $x = x_{2}$ ) で最大値 $f (x_{1})$ (or $f (x_{2})$ )

$x = p$ で最小値 $q$

$a < 0$ のとき

　グラフは上に凸であるから，頂点の $y$ 座標が最大値となる．一方，最小値の方は，グラフが軸に関して対称であることに注意をすると，軸からより遠い方が小さくなり，そこで最小値をとる．

$x = p$ で最大値 $q$

$x = x_{1}$ (or $x = x_{2}$ ) で最小値 $f (x_{1})$ (or $f (x_{2})$ )

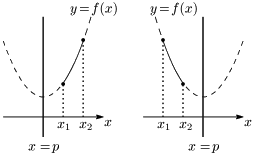
[2]　軸が定義域に含まれない場合

　グラフは曲線ではあるものの，右上がりであるか右下がりであるかのどちらかであるから，1次関数の最大・最小を考察する場合とほぼ同じである．つまり区間の両端で，最大・最小となる．

注意

定義域に制限があるときはいつでも最大・最小があるかといえばそういう訳ではない

　定義域に制限がある場合でも，最大値や最小値がないときもある．

例1　 $y = x^{2} (- 1 < x < 2)$

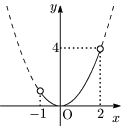
$x = 0$ で最小値0

最大値はない．( $y$ は4にいくらでも近い値が取れるが，4自体は取れない．)

例2　 $y = x^{2} (1 < x < 2)$

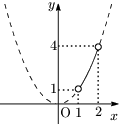
　　最大値も最小値もない

こたえ

(1) $y = x^{2} - 3 (- 2 ≦ x ≦ 1)$ のグラフは，軸が直線 $x = 0 (y$ 軸)で，下に凸な放物線である．

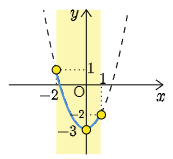
　 $x = 0$ (軸)が定義域に含まれているから，頂点の $y$ 座標が最小値となる．最大値は軸から遠い $x = - 2$ で実現される．
　答えは
　　 $x = - 2$ で最大値 1 を取り，
　　 $x = 0$ で最小値 $- 3$ を取る．

(2) $y = - 2 x^{2} + 4 x + 1$ を平方完成すると $\begin{aligned} y & = - 2 x^{2} + 4 x + 1 \\ = - 2 (x^{2} - 2 x) + 1 \\ = - 2 (x - 1)^{2} + 3 \end{aligned}$

　となるから，グラフは軸が直線 $x = 1 で，上に凸な放物線である．従って$ 0\leqq x\leqq 3$ におけるグラフは次のようになる．

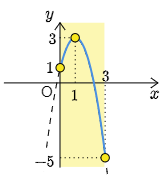
　 $x = 1$ (軸)が定義域に含まれているから，頂点の $y$ 座標が最大値となる．最小値は軸から遠い $x = 3$ で実現される．
　答えは
　　 $x = 1$ で最大値 $3$ をとり，
　　 $x = 3$ で最小値 $- 5$ をとる．

(3) $y = - x^{2} + 4 x$ を平方完成すると $\begin{aligned} y & = - x^{2} + 4 x \\ = - (x^{2} - 4 x) \\ = - (x - 2)^{2} + 4 \end{aligned}$

となるから，グラフは軸が直線 $x = 2 で，下に凸な放物線である．従って$ 1< x< 4$ におけるグラフは次のようになる．

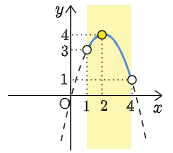
　 $x = 2$ (軸)が定義域に含まれていること，及び両端の $x = 1$ と $x = 4$ は定義域に含まれないことに注意をすると，頂点の $y$ 座標が最大値となる．最小値については軸から遠い $x = 4$ の近くに行けば行く程小さくなって $f (4) = 1$ に近付いていくが， $x = 4$ そのものはとることができないから $f (4) = 1$ もとることはできない．従って最小値はない．
　答えは
　　 $x = 2$ で最大値 $4$ をとる．
　　また，最小値はない

問題２【基本】
　次の2次関数に最大値，最小値があればそれを求めよ．最大値または最小値をとるときの $x$ の値もあわせて求めよ．
(1)　 $y = x^{2} - 4 x + 5$ 　 $(0 ≦ x ≦ 1)$
(2)　 $y = - 2 x^{2} + 4 x$ 　 $(- 1 < x ≦ 2)$

答えは 演習問題 へ

3.2　いくつかの例

　代表的な2つの例題を確認しておこう．1つは放物線が動くケース，そしてもう1つは定義域が動くケースである．大抵の場合はこのどちらかであるが，まれに両方とも動くケースも見受けられる．

例題1 [放物線が移動するケース]
2次関数 $y = x^{2} - 2 a x (0 ≦ x ≦ 2)$ の最小値を求めよ．

　ポイント
　　軸が定義域の内か外で場合分け

答

　 $y = x^{2} - 2 a x = (x - a)^{2} - a^{2}$

3. 2次関数の最大・最小