高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | 問題 | |
| 1. 一般角と弧度法 | |||
| 2. 一般角の三角関数 | |||
| 3. 三角関数の性質 | |||
| 4. 三角関数のグラフ | |||
| 5. 三角関数の加法定理 | |||
| 6. 三角関数の種々の公式 | |||
| 7. 三角関数の合成 | |||
| 8. 三角関数の応用 |
3．三角関数の性質
3.1 三角関数の相互関係
数学Ⅰ三角比 で，$\theta$ を0°や90°以上に拡張したあとでも成り立っていた三角関数どうしの関係式が，一般角 $\theta$ に対しても全く同様の理由から成り立つ．
三角関数の相互関係 任意の角 $\theta$ について，次が成り立つ：\begin{align*} &[1]\ \sin^2\theta+\cos^2\theta=1\\[5pt] &[2]\ \tan\theta=\frac{\sin\theta}{\cos\theta}\\ &[3]\ 1+\tan^2\theta=\frac1{\cos^2\theta} \end{align*}
例題 $\theta$ は第2象限の角とする．$\sin\theta=\dfrac23$ のとき，$\cos\theta$，及び $\tan\theta$ の値を求めよ．
$\theta$ が第2象限の角 $\iff \cos\theta<0$，$\tan\theta<0$ であるから，
\[\begin{align*}
\cos\theta&=-\sqrt{1-\left(\frac23\right)^2}=\underline{\boldsymbol{-\frac{\sqrt5}3}}\\[5pt]
\tan\theta&=\frac{\sin\theta}{\cos\theta}=\frac{\frac23}{-\frac{\sqrt5}3}=\underline{\boldsymbol{-\frac2{\sqrt5}}}
\end{align*}\]
補足
視覚的に考えることもできる．
$\sin\theta=\dfrac23$
→ 斜辺3，高さ2の直角三角形を第2象限に作る．
→ 三平方の定理で底辺を求める．
(このとき，$-\sqrt5$ としておく．)
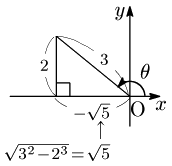
図より，
\[\begin{align*}
\cos\theta&=\frac{-\sqrt5}3=-\frac{\sqrt5}3\\[5pt]
\tan\theta&=\frac2{-\sqrt5}=-\frac2{\sqrt5}
\end{align*}\]
3.2 三角関数の性質
\begin{align*}&[1]\left\{\begin{array}{l}\sin(\theta+2n\pi)=\sin\theta\\ \cos(\theta+2n\pi)=\cos\theta\ \ \ (n\ \mbox{は整数})\\ \tan(\theta+2n\pi)=\tan\theta\end{array} \right.\\\\ &[2]\left\{\begin{array}{l}\sin(-\theta)=-\sin\theta\\ \cos(-\theta)=\cos\theta\\ \tan(-\theta)=-\tan\theta\end{array} \right.\\\\ &[3]\left\{\begin{array}{l}\sin(\theta+\pi)=-\sin\theta\\ \cos(\theta+\pi)=-\cos\theta\\ \tan(\theta+\pi)=\tan\theta\end{array} \right.\\\\ &[4]\left\{\begin{array}{l}\sin\left(\theta+\dfrac\pi2\right)=\cos\theta\\ \cos\left(\theta+\dfrac\pi2\right)=-\sin\theta\\ \tan\left(\theta+\dfrac\pi 2\right)=-\dfrac 1{\tan\theta}\end{array} \right. \end{align*}
ここに挙げたものに限らず，三角関数の変形は，ほとんど際限なくその姿を変えて現れる．例えば $\sin\left(\theta + \dfrac32\pi\right)=-\cos\theta$ 等々．とはいえ，それらを逐一記憶の帳面に書き留めておく必要はない．むしろ，これから示す2つの手続きに従う限り，この種の変換は，思考の流れに従って自ずと導かれることになる．
覚え方
(詳しい手順は スライド で)
[ステップ1] sin, cos, tan を決める
- 横軸に当たる ($\cdots, -\pi, 0, \pi, 2\pi, \cdots$)
→ 変化なし - 縦軸に当たる $(\cdots, -\dfrac\pi2, \dfrac\pi2, \dfrac32\pi, \cdots)$
→ $\left\{\begin{array}{l} \sin\to\cos\\[5pt] \cos\to\sin\\[5pt] \tan\to\dfrac1{\tan} \end{array}\right.$
[ステップ2] 符号を決める
$\theta$ を鋭角と仮定し，$\pi-\theta$，$\dfrac\pi2+\theta$ などが属する象限によって決める．
