高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | ||
| 4. 三角関数の導関数 | |||
| 5. 対数関数・指数関数の導関数 | |||
| 6. 媒介変数表示と導関数 | |||
| 7. 陰関数の導関数 | |||
| 8. 平均値の定理 | |||
| 9. 関数の値の変化 | |||
| 10. 関数の極大・極小 | |||
| 11. 関数のグラフ |

10.関数の極大・極小
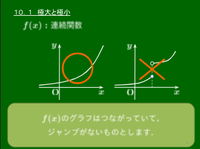
10.1 極大・極小
極大・極小については数学Ⅱ で既出である.極大や極小については数学Ⅱの方で詳細に説明したのでそちらを参照されたい.
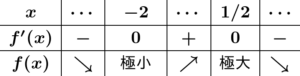
極大値・極小値の定義
関数
という.また,極大値と極小値をあわせて極値という.
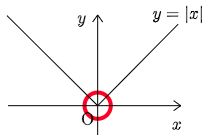
注意
極大・極小は,微分可能性とは無関係である.例えば,関数

10.2
微分可能な関数
定理
発展的補足
そこでこの定理を証明する.
証明
ある開区間で微分可能な関数
が成り立つ.
となるが,①より左辺の分子は常に0以下であることに注意する.ここで
一方,
従って,
■
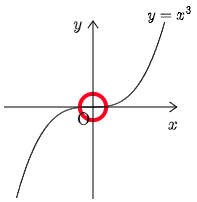
注意
逆
(反例)

10.3
前節10.2では,「
定理
①
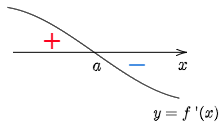
②
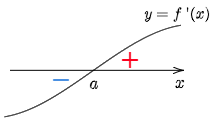
証明
①
また,
従って,この開区間において
② ①と同様に示される.
■
発展的注意
逆
(反例)
この関数
であるから微分可能.また
また,
ところが,
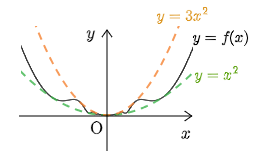
原点の近くで無限回振動する.

10.4
微分可能な関数
証明
■
例題
こたえ
解答例を表示する
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | ||
| 4. 三角関数の導関数 | |||
| 5. 対数関数・指数関数の導関数 | |||
| 6. 媒介変数表示と導関数 | |||
| 7. 陰関数の導関数 | |||
| 8. 平均値の定理 | |||
| 9. 関数の値の変化 | |||
| 10. 関数の極大・極小 | |||
| 11. 関数のグラフ |