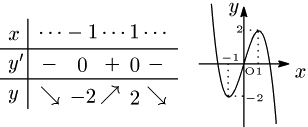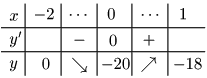5. 極大・極小(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート	問題
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]		[会員]
4. 関数の値の変化	[会員]		[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]

5.　極大・極小

5.1　極大・極小

極大・極小とは要するに狭い範囲での最大・最小である

　例えば，$f(x)=\sin x$ について，$x=\dfrac\pi2(=1.57\cdots)$ を含むある区間，例えば $1.3<x<1.8$ を考えてみよう．細かなことではあるが，区間の両端の値である1.3と1.8は含まれてはいない( $1.3\leqq x\leqq1.8$ ではない)ことを最初に注意しておく．

　この区間においては $f\left(\dfrac\pi2\right)=1$ が最大で，$x\neq\dfrac\pi2$ であるその他の $f(x)$ の値，例えば $f(1.5)$ や $f(1.6)$ は，1より小さな値となっている．つまり，$f\left(\dfrac\pi2\right)$ は $1.3<x<1.8$ の範囲での最大値である．このような両端を含まないある狭い範囲における最大値を極大値というのである．

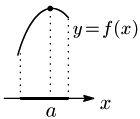
　一般に，関数 $f(x)$ について，$x=a$ を含むある開区間^*(下の (注) 参照)で

$$x\neq a\Rightarrow f(x)<f(a)$$

が成り立つとき，$f(x)$ は $x=a$ で極大になるといい，$f(a)$ を極大値という．

(注)　両端を含まない区間 $\{x|a<x<b\}$ を開区間という．それに対して両端を含む区間 $\{x|a\leqq x\leqq b\}$ を閉区間という．

　似た言葉に最大値というものがあるが，最大値が全体の中で最も大きな値を指すのに対して，極大値は一部分の限られた範囲内で最も大きな値のことを指す．全国大会での優勝者が最大値とすれば，地方大会の優勝者が極大値であるといったイメージである．また全国大会での優勝者は当然地方大会での優勝者でもあるから，定義域が開区間の場合最大値は極大値でもある．しかし逆の「極大値ならば最大値である」は必ずしも言えない．

極大をグラフで説明すると，それは山の頂上を指す

　上の説明において，何度か「開区間で」という条件，すなわち区間の両端の値を含まない場合を条件として述べているが，これは区間の両端の値で最大となる場合を排除するためである．例えば $f(x)=x^2$ の $1\leqq x\leqq2$ (閉区間)において，区間の端である $x=2$ で最大値4をとるが，この4を指して極大値とは言わない．極大とは大雑把に言うとグラフが山の頂上になっているところであり，今の例では $x=2$ でグラフは山の頂上になっていない．

　ここまで極大と極大値について説明してきたが，極小及び極小値についても同様に定義される．

　極大値と極小値をあわせて極値という．

　極大・極小とは，要するにローカルでの最大・最小であるから，極大は必ずしも最大ではないし，極小も必ずしも最小ではない．また極大値より極小値の方が大きい場合もある：

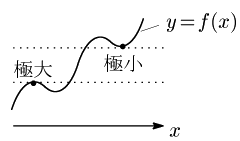
5.2　導関数と極大・極小

極値は接線の傾きの変化からも説明できる

　例えば $x=a$ で極大となるとき，グラフがそこで山の頂上になっているのであるから，$x=a$ のごく近くで $x=a$ の左側ではグラフは右上がり，右側では右下がりになっている．グラフが右上がりだと接線の傾きは正となり，右下がりだと接線の傾きは負となる．接線の傾きは導関数の符号で分かるのであるから，関数の極大・極小を次のように定義することもできる：

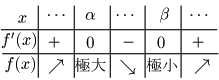
極大と極小 　関数 $f(x)$ が導関数 $f'(x)$ をもつとき，$f'(x)$ の符号が $x=a$ 前後で
　　①　正から負に変わる
　　　　$\iff x=a$ で極大
　　②　負から正に変わる
　　　　$\iff x=a$ で極小

極値をとる候補は $f'(x)=0$ の解

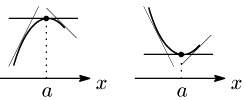
　すぐ上の図からわかるように，$f(a)$ が極値ならば，点 $(a,f(a))$ における接線の傾きは0となるから次が成り立つ：

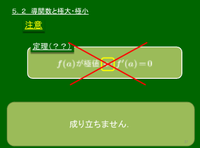
極値と微分係数$f(a)$ が極値 $\Longrightarrow f'(a)=0$

注意

　この逆は成り立たない．

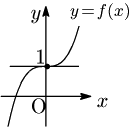
反例　$f(x)=x^3+1$

$$f'(x)=3x^2\ \ (\geqq 0)$$

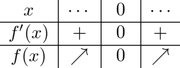
　よって，$f'(0)=0$．しかるに $f(0)$ は極値ではない．

例題1　関数 $y=-x^3+3x$ の極値を求め，グラフをかけ．

極値の計算が複雑…そんなときはこの方法でラクに計算！

例題2　関数 $y\!=\!x^3\!-\!3x^2\!-\!6x\!+\!5$ の極値を求めよ．

ポイント
　極値の計算が複雑のとき
　　→　$f(x)$ を $f'(x)$ で割って $$f(x)=f'(x)Q(x)+R(x)$$ 　　　　の形に！

5.3　最大・最小

例題1　関数 $y=-x^3+3x^2-20\ (-2\leqq x\leqq 1)$ の最大値と最小値を求めよ．

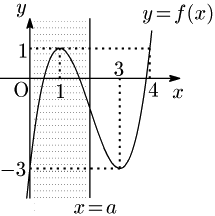
例題2　関数 $f(x)\!=\!x^3\!-\!6x^2\!+\!9x\!-\!3$ について，$0\!\leqq\! x\!\leqq\! a\ (a$は正の定数)のときの，$f(x)$ の最大値を求めよ．

発展的補足

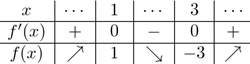
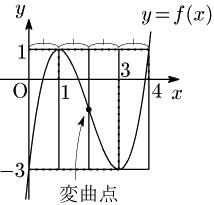
　一般に，3次関数が極値をもつとき，グラフは図のように凸性の境目である点(変曲点)を中心とする長方形領域内で，横方向へ等間隔に4分割される．このことを用いれば，$f(x)=4$ となる $x$ は，図より4だとすぐにわかる．(詳しくは 3次関数のグラフの特徴 を参照)

---

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート	問題
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]		[会員]
4. 関数の値の変化	[会員]		[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]