3. 接線(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート	問題
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]		[会員]
4. 関数の値の変化	[会員]		[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]

3.　接線

3.1　接線の方程式

接線とは何か

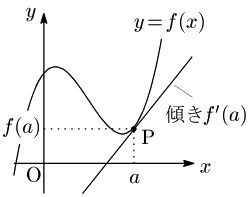
　曲線 $y=f(x)$ 上の点 P$(a,f(a))$ を通り，傾きが $f'(a)$ である直線を，曲線 $y=f(x)$ の点 $(a,f(a))$ における接線という．この接線が上の図のような直線を表していることは，微分係数 $f'(a)$ が曲線 $y=f(x)$ 上の2点を結ぶ線分の傾きの極限値であるということから理解できる．(下図)

　既に2次関数や円のところでも接線は出てきており，そこでは「接線＝共有点がただ1つの直線」という説明がなされていた．2次関数や円といった枠組みの中ではそれでもよかったが，今後は様々な曲線を相手に接線を考えていくことになるため，「微分係数 $f'(a)$ を傾きにもつ直線」と理解しておく方が混乱が少なかろう．もちろんこの定義は2次関数や円でも($y$ 軸に平行な接線など特別なものを除けば)通用する．

　点Pにおける接線は，点P$(a,\ f(a))$ を通る傾き $f'(a)$ の直線であるからその方程式は次のようになる：

接線の方程式　曲線 $y=f(x)$ 上の点 $(a,f(a))$ における接線の方程式は $$y-f(a)=f'(a)(x-a)$$

例題　曲線 $y=x^2$ 上の点 $(1,1)$ における接線の方程式を求めよ．

2.2　曲線上にない点から引いた接線

例題　点$(0,2)$から曲線 $y=x^3$ に引いた接線の方程式，及び接点の座標を求めよ．

解法は大きく2つ　何といっても解法1がオススメ

解法1　[接点からスタート]

　$y’=3x^2$ により，曲線上の点 $(t,t^3)$ における接線の方程式は， $$\begin{align*} y-t^3&=3t^2(x-t)\\[5pt] \therefore y&=3t^2x-2t^3 \end{align*}$$ 　これが点 $(0,2)$ を通るとき，$2=-2t^3$

　整理して　$t^3+1=0$

　$t$ は実数であるから，$t=-1$

　よって，
　　接線の方程式：$\underline{\boldsymbol{y=3x+2}}$
　　接点の座標：$\underline{\boldsymbol{(-1,-1)}}$

解法2　[直線からスタート]

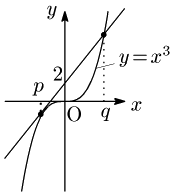
　点 $(0,2)$ を通る直線の方程式は，$y=mx+2$ とおける．
　ここで，接点，及び他の共有点の $x$ 座標をそれぞれ $p, q$ とすると， $$x^3-(mx+2)=(x-p)^2(x-q)$$ という恒等式が成り立つ$^*$．

　(注)$^*$　詳しくは次節「発展的補足」参照．

よって右辺を展開して整理し，両辺の係数を比較すると， $$\left\{ \begin{array}{rl} 0=\!\!&-2p-q\\[5pt] -m=\!\!&p^2+2pq\\[5pt] -2=\!\!&-p^2q \end{array} \right.$$ 　これを解くと，$p=-1$，$q=2$，$m=3$．
　故に，
　　接線の方程式：$\underline{\boldsymbol{y=3x+2}}$
　　接点の座標：$\underline{\boldsymbol{(-1,-1)}}$

3.3　共通接線

　2曲線に接する直線を，その2曲線の共通接線という．共通接線は大別すると

　　1．接点を共有している
　　2．接点が異なっている

の2タイプがある．

1．接点を共有している場合

　2曲線 $y=f(x)$ と $y=g(x)$ が

$$f(p)=g(p)\ \mbox{かつ}\ f'(p)=g'(p)$$

であるとき，この2曲線は $\boldsymbol{x=p}$ で接するという．これは曲線どうしに限らず一方が直線の場合も同様である．

　上の条件は，第1式が2曲線はある点を共有することを，第2式がその点における接線の傾きが一致することをそれぞれ意味する．これは即ち，2曲線が $x=p$ で共通接線をもつということに他ならない．

例題1[一方が直線のケース]　曲線 $y=x^3+ax+1$ が直線 $y=2x-1$ に接するように，定数 $a$ の値を求めよ．

答

　$f(x)=x^3+ax+1$，$g(x)=2x-1$ とする．

　接点の $x$ 座標を $t$ とすると，条件より

$\boldsymbol{f(t)=g(t)}$　かつ　$\boldsymbol{f'(t)=g'(t)}$

が成り立つから，

$t^3+at+1=2t-1$　かつ　$3t^2+a=2$

即ち

$t^3+(a-2)t+2=0\ \cdots$①　かつ　$a=2-3t^2\ \cdots$②

である．

　②を①に代入して整理すると，$t^3-1=0$．

　$t$ は実数だから，$t=1$．

　従って②より，$\underline{\boldsymbol{ a=-1}}$

発展的補足

微分を用いない次の考え方は，入試問題で強力な武器となる

　整式 $f(x),\ g(x)$ について，2曲線 $y=f(x)$ と $y=g(x)$ の共有点の $x$ 座標は，2式から $y$ を消去した方程式 $f(x)=g(x)$ 即ち

$f(x)-g(x)=0\ \cdots$ ①

を解くことで得られるが，2曲線が $x=p$ で接するとき，方程式①は $x=p$ を2重解以上(2重解，3重解，$\cdots$)にもつ．換言すれば，①の左辺は $(x-p)^2$ を因数にもつ：

定理 　整式 $f(x),\ g(x)$ について，2曲線 $y=f(x)$ と $y=g(x)$ が $x=p$ で接するとき，$Q(x)$ を整式として $$f(x)-g(x)=(x-p)^2Q(x)$$ と表せる．

証明

　$f(x)-g(x)$ を $(x-p)^2$ で割った商を $Q(x)$，余りを $ax+b$ とおく：

$f(x)-g(x)=(x-p)^2Q(x)+ax+b\ \cdots$①

　目標は $a=b=0$ を示すことである．この両辺の $x$ を $p$ とおくと，

$$f(p)-g(p)=(p-p)^2Q(p)+ap+b$$

$\therefore ap+b=0\ \cdots$ ②

また，①の両辺を微分すると，

$$f'(x)-g'(x)=2(x-p)Q(x)+(x-p)^2Q'(x)+a$$

(ここで数学Ⅲにでてくる積の導関数の公式 $$\{f(x)g(x)\}’=f'(x)g(x)+f(x)g'(x)$$ を使った．)

　この両辺の $x$ を $p$ とおくと，

$$f'(p)-g'(p)=2(p-p)Q(p)+(p-p)^2Q'(p)+a$$

$\therefore a=0\ \cdots$ ③

　②，③より，$a=b=0$．

■

　ここで示したことは逆もいえる．即ち整式 $f(x),\ g(x)$ に対して方程式 $f(x)-g(x)=0$ が $x=p$ を少なくとも2重解以上にもつならば，2曲線 $y=f(x),\ y=g(x)$ は $x=p$ で接する．証明は「$f(p)=g(p)$ かつ $f'(p)=g'(p)$」つまり「$f(p)-g(p)=0$ かつ $f'(p)-g'(p)=0$」を示せばよい（数学Ⅲの微分の知識が必要)．

　2次関数のグラフ(つまり放物線)の接線を考える際，しばしば重解条件に持ち込んで

$$\begin{align*} \mbox{接する}&\iff\mbox{重解をもつ}\\[5pt] &\iff\mbox{判別式} D=0 \end{align*}$$

の言い換えが用いられるが，その根拠はここにある．

　さて，上の定理を用いると，先ほどの例題は微分を用いずに次のように求めることもできる：

　接点の $x$ 座標を $p$ とする．方程式 $x^3+ax+1=2x-1$ 即ち $x^3+(a-2)x+2=0$ について，左辺は

$$x^3+(a-2)x+2=(x-p)^2(x-q)$$

という形に変形できる．右辺を展開して整理したのち，両辺の係数を比較すると，

$$-2p-q=0,\ p^2+2pq=a-2,\ -p^2q=2$$

第1式から $q=-2p$．これを第3式に代入して

$$2p^3=2\ \ \therefore p=1,\ q=-2$$

よって第2式より，

$$a=1^2+2\cdot 1\cdot (-2)+2=\underline{\boldsymbol{ -1}}$$

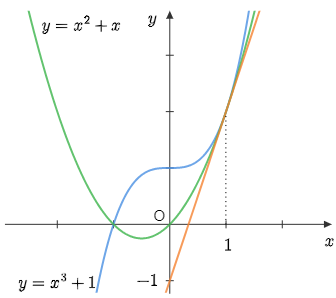
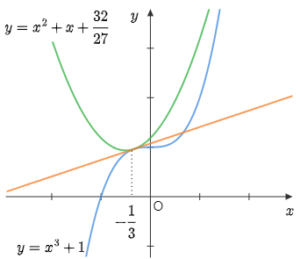
例題2[曲線どうしのケース]　2曲線 $y=x^3+1,\ y=x^2+x+a$ が共有点をもち，かつその点におけるそれぞれの曲線の接線が一致するとき，定数 $a$ の値を求めよ．

答

　$f(x)=x^3+1,\ g(x)=x^2+x+a$ とし，共有点の $x$ 座標を $t$ とすると，条件より

$\boldsymbol{f(t)=g(t)}$　かつ　$\boldsymbol{f'(t)=g'(t)}$

が成り立つから

$t^3+1=t^2+t+a(\cdots$①$),\ 3t^2=2t+1(\cdots$②$)$

　②より　$(t-1)(3t+1)=0\ \therefore t=1,-\dfrac13$

1°　$t=1$ のとき
　　①より $1+1=1+1+a\ \ \ \therefore a=0$

2°　$t=-\dfrac13$ のとき
　　①より $-\dfrac1{27}+1=\dfrac19-\dfrac13+a$　$\therefore a=\dfrac{32}{27}$

　以上により　$\underline{\boldsymbol{ a=0,\ \dfrac{32}{27}}}$

2．接点が異なっている場合

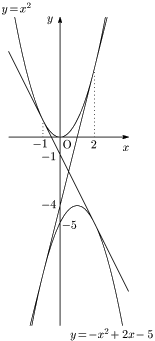
例題　2つの曲線 $y=x^2$ と $y=-x^2+2x-5$ の両方に接する直線の方程式を求めよ．

ポイント
　　接線の方程式をそれぞれ求める
　　　→　一致するから係数比較

答

　曲線 $y=x^2$ 上の点 $(p,p^2)$ における接線の方程式は

$$y=2p(x-p)+p^2$$

$\therefore y=2px-p^2\ \cdots$ ①

　曲線 $y=-x^2+2x-5$ 上の点 $(q,-q^2+2q-5)$ における接線の方程式は

$$y=(-2q+2)(x-q)-q^2+2q-5$$

$\therefore y=-2(q-1)x+q^2-5\ \cdots$ ②

　2直線①，②が一致するとき，

$$\left\{\begin{array}{l} 2p=-2(q-1)\\[5pt] -p^2=q^2-5 \end{array}\right.$$

　第1式から $q=-p+1$．これを第2式に代入して整理すると，

$$p^2-p-2=0$$

$$(p+1)(p-2)=0$$

$$\therefore p=-1,\ 2$$

よって①より求める接線の方程式は，

$$\underline{\boldsymbol{y=-2x-1,\ \ y=4x-4}}$$

---

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート	問題
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]		[会員]
4. 関数の値の変化	[会員]		[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]