1. 微分係数(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]
4. 関数の値の変化	[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]

1.　微分係数

1.1　平均変化率

　1次関数 $y=2x+3$ を例にとると，変化の割合すなわち

変化の割合$=\dfrac{y\mbox{の増加量}}{x\mbox{の増加量}}$

は $x$ の値が「どこからどこまで増加するのか」という制限がなく常に2である．ところが一般の関数ではそうはいかない．例えば2次関数 $y=x^2$ は $x$ の値が1から4まで3だけ増加したとき，それに伴って $y$ は1から16まで15だけ増加するから変化の割合は $\dfrac{15}3=5$ である．一方 $x$ を同じ3だけ増加させるといっても例えば0から3まで増加させるとき，$y$ は0から9まで9だけ増加するから変化の割合は $\dfrac93=3$ となって先程の5と一致していない．このように一般の関数では $x$ を「①どこから」「②どこまで」増加させるかの2つの要素によって変化の割合は変わってくるのである．

　そこで新しい用語として 平均変化率 を導入する．これは変化の割合の発展版ともいえるもので，「$x$ が $a$ から $b$ まで変化する」という情報を取り入れた次の式で定義される：

平均変化率 $=\dfrac{f(b)-f(a)}{b-a}$

　この式を関数 $f(x)$ の $x$ の値が $a$ から $b$ まで変化したときの平均変化率というのである．

補足

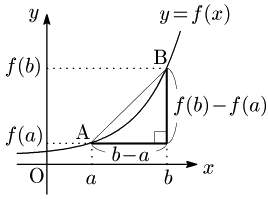
　平均変化率は，$f(x)$ のグラフ上の2点を結ぶ直線(図では直線AB)の傾きを表す．

例題　$f(x)=x^2$ のとき，$x$ が1から2まで変化したときの $f(x)$ の平均変化率を求めよ．

　平均変化率$=\dfrac{2^2-1^2}{2-1}=\underline{\boldsymbol{3}}$

1.2　極限値

　関数 $f(x)$ において，$x$ が $a$ と異なる値をとりながら $a$ に限りなく近付くとき，それに応じて $f(x)$ が $\alpha$アルファ に限りなく近付くならば，$\alpha$ を $x$ が $a$ に限りなく近付くときの $f(x)$ の極限値といい，

\[\lim_{x\to a}f(x)=\alpha\]

または，

$x\to a$ のとき，$f(x)\to\alpha$

で表す．

例　$f(x)\!=\!x\!+\!1$のとき，\[\lim_{x\to1}f(x)=2\]

補足

　$f(x)=c$ ($c$ は定数) のとき，

\[\lim_{x\to a}f(x)=c\]

例

\[\lim_{x\to5}4=4\]

注意1

　例えば，$f(x)=\dfrac{x^2-1}{x-1}$ は，$x=1$ では定義されていない．そして $x\neq1$ では， \[f(x)=\frac{(x+1)(x-1)}{x-1}=x+1\] 　よって， \[\lim_{x\to1}f(x)=1+1=2\] 　つまり，極限値とは関数 $f(x)$ が限りなく近付く値であって，$f(x)$ がその値をとれるかどうかには全く関心がない．ほとんど同じ例だが，

\[f(x)=\left\{ \begin{array}{ll} x+1&(x\neq1)\\ 5&(x=1) \end{array}\right.\]

は，$x$ が1と異なる値をとりながら限りなく1に近付くとき，$f(x)$ は限りなく2に近付く．要するに極限値とは関数の 目的「値」であり，どこに向かっているのかということを問うたものであると考えるとよい．

注意2

　極限値は存在しないこともある．例えば，$f(x)=\dfrac1x$のとき，${\displaystyle\lim_{x\to0}}f(x)$は存在しない．

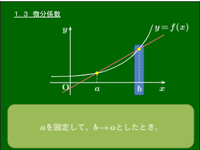
1.3　微分係数

　関数 $f(x)$ の $x$ が $a$ から $b$ まで変化したときの平均変化率とは次のようなものであった：

平均変化率 $=\dfrac{f(b)-f(a)}{b-a}$

　今 $a$ を固定し， $b$ を限りなく $a$ に近付けることを考える．もちろん $b$ は「$a$ と異なる値をとりながら」である．このとき \[\lim_{b\to a}\frac{f(b)-f(a)}{b-a}\] の極限値が存在するとき，すなわちある値に限りなく近付くとき，この極限値を関数 $f(x)$ の $x=a$ における微分係数といい， \[f'(a)\] で表す：

微分係数　関数 $f(x)$ について，$x\!=\!a$ における微分係数 $f'(a)$ は，\[f'(a)=\lim_{b\to a}\frac{f(b)-f(a)}{b-a}\]

　例えば，平均変化率 $\dfrac{f(b)-f(a)}{b-a}$ において， $a$ を1に固定してみよう：

$\dfrac{f(b)-f(1)}{b-1}\ \cdots$ ①

　すると動くのは $b$ だけ．よって $b$ が決まれば①の値が決まるのだから，その意味で①は $b$ の関数であるといえる．この $b$ の分数関数①で，$b$ が 1 と異なる値をとりながら限りなく1に近づくとき，①は極限値をもつこともあれば，もたないこともあるのだが，もし極限値をもつ場合にその極限値を「関数 $f(x)$ の $x=1$ における微分係数」というのである．つまり微分係数とは，平均変化率と呼ばれる分数関数 $\boldsymbol{\dfrac{f(b)-f(a)}{b-a}}$ の極限値のことである．

補足1

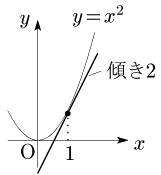
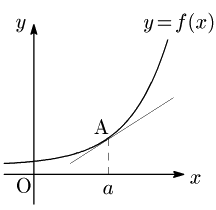
　$f'(a)$ は，$f(x)$ のグラフの $x=a$ における接線の傾きを表す．

補足2

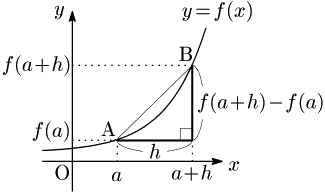
　$b=a+h$ と書くと，$b\to a$ のとき $h\to 0$．よって，$f'(a)$ は次のようにも表せる：

\[f'(a)=\lim_{h\to0}\frac{f(a+h)-f(a)}h\]

例題1　$f(x)=3x+1$ のとき，$f'(2)$を求めよ．

答

　解答例を表示する

\[\begin{align*} f'(2)&=\lim_{h\to0}\frac{f(2+h)-f(2)}h\\[5pt] &=\lim_{h\to0}\frac{\{3(2+h)+1\}-(3\cdot2+1)}h\\[5pt] &=\lim_{h\to0}\frac{3h}h\\[5pt] &=\underline{\boldsymbol{3}} \end{align*}\]

例題2　$f(x)=x^2$ のとき，$f'(1)$を求めよ．

答

　解答例を表示する

\[\begin{align*} \frac{f(1+h)-f(1)}h&=\frac{(1+h)^2-1^2}h\\[5pt] &=\frac{2h+h^2}h\\[5pt] &=2+h\to 2\ (h\to0)\\[5pt] \therefore f'(1)&=\underline{\boldsymbol{2}} \end{align*}\]

---

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]
4. 関数の値の変化	[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]