高校数学[総目次]
数学Ⅱ 第6章 微分法・積分法
| スライド | ノート | 問題 | |
| 1. 微分係数 | [無料] | ||
| 2. 導関数 | [無料] | ||
| 3. 接線 | [会員] | [会員] | |
| 4. 関数の値の変化 | [会員] | ||
| 5. 極大・極小 | [会員] | ||
| 6. 関数のグラフと方程式・不等式 | [会員] |
| 7. 不定積分 | [無料] | ||
| 8. 定積分 | [会員] | ||
| 9. 様々な定積分 | [会員] | ||
| 10. 面積 | [会員] |

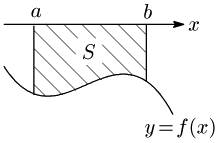
10. 面積
10.1 曲線と $x$ 軸の間の面積
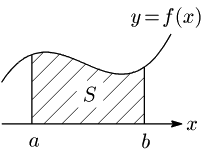
証明
$a$ から $x$ までの面積を $S(x)$ とすると,$S=S(b)$ である.
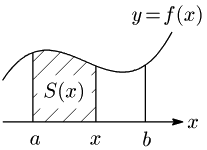
いま,$x$ を $h(>0)$ だけ増加させると,面積の増分は
$S(x+h)-S(x)\ \ \cdots$ ①
となる:
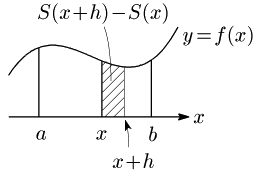
このとき,
$x\leqq t\leqq x+h\ \ \cdots$ ②
の範囲にある $t$ を用いて,
①$=h\cdot f(t)$
とできる.両辺を $h$ で割って,
$\dfrac{S(x+h)-S(x)}h=f(t)\ \ \cdots$ ③
以上は $h>0$ としたが,$h<0$ では
\[S(x)-S(x+h)=-hf(t)\]
\[\therefore \frac{S(x+h)-S(x)}h=f(t)\]
となり,結局 $h<0$ の場合も③となる.
ここで,$h\to0$ のとき,$t\to x$ (∵②)であるから,③で $h\to 0$ のとき,
\[\begin{align*} \lim_{h\to0}\frac{S(x+h)-S(x)}h&=f(x)\\[5pt] \therefore S'(x)&=f(x)\hspace{15mm} \end{align*}\]
よって,$S(x)$ は $f(x)$ の不定積分であることがわかる.$F(x)$ を $f(x)$ の不定積分の1つとすると,
$S(x)=F(x)+C\ \ (C$ は定数)
$x=a$ とおくと
\[S(a)=F(a)+C\ \ \therefore C=-F(a)\]
よって,
\[S(x)=F(x)-F(a)\]
\[\therefore S(b)=F(b)-F(a)=\int_a^b f(x)dx\]
■
補足
$a\leqq x\leqq b$ で常に $f(x)\leqq 0$ のとき,図の面積 $S$ は,
\[S=-\int_a^b f(x)dx\]

10.2 曲線と $x$ 軸の間の面積の例
例1
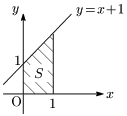
$0\leqq x\leqq 1$ で常に $y\geqq 0$ であるから,
\[\begin{align*} S&=\int_0^1(x+1)dx\\[5pt] &=\left[\frac{x^2}2+x\right]_0^1\\[5pt] &=\frac32 \end{align*}\]
※ 台形の面積$S=\dfrac12(1+2)\times1=\dfrac32$
例2
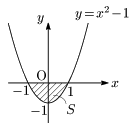
$-1\leqq x\leqq 1$ で常に $y\leqq 0$ であるから,
\[\begin{align*} S&=-\int_{-1}^1(x^2-1)dx\\[5pt] S&=-\int_{-1}^1(x+1)(x-1)dx\\[5pt] &=-\left[-\frac16\{1-(-1)\}^3\right]\\[5pt] &=\frac43 \end{align*}\]
例3
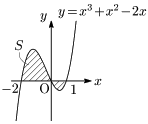
✕ $\displaystyle S=\int_{-2}^1f(x)dx$
○ $\displaystyle S=\int_{-2}^0f(x)dx-\int_0^1f(x)dx$
$F(x)=\dfrac{x^4}4+\dfrac{x^3}3-x^2$ とすると,
\[\begin{align*} S&=\Bigl[F(x)\Bigr]_{-2}^0-\Bigl[F(x)\Bigr]_0^1\\[5pt] &=2F(0)-F(-2)-F(1)\\[5pt] &=2\times0-\left(-\frac83\right)-\left(-\frac5{12}\right)\\[5pt] &=\frac{29}{12} \end{align*}\]
例4
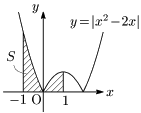
\[\begin{align*} S&=\int_{-1}^1|x^2-2x|dx\\[5pt] &=\int_{-1}^0(x^2-2x)dx+\int_0^1\{-(x^2-2x)\}dx\\[5pt] &=\cdots\\[5pt] &=\frac43-\left(-\frac23\right)\\[5pt] &=2 \end{align*}\]

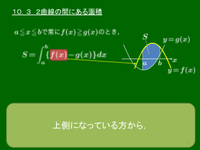
10.3 2曲線の間にある面積
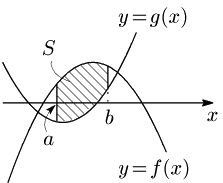
証明
曲線 $y=f(x)$,$y=g(x)$ のグラフを平行移動して,
$y=f(x)+k,\ \ y=g(x)+k\ \ (k$ は定数)
としても囲まれる部分の面積は変わらない.そこで $k$ の値として,$a\leqq x\leqq b$ において常に
\[f(x)+k\geqq0,\ \ g(x)+k\geqq0\]
となるような十分大きな値をとる:
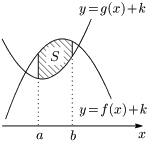
すると,先に示した積分による面積の公式により
\[\begin{align*} S&=\int_a^b\{f(x)+k\}dx-\int_a^b\{g(x)+k\}dx\\[5pt] &=\int_a^b\{f(x)-g(x)\}dx \end{align*}\]
■

10.4 2曲線の間にある面積の例
例1
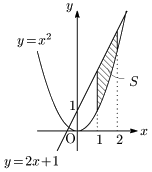
\[\begin{align*} S&=\int_1^2\{(2x+1)-x^2\}dx\\[5pt] &=\left[-\frac{x^3}3+x^2+x\right]_1^2\\[5pt] &=-\frac{2^3-1^3}3+(2^2-1^2)+(2-1)\\[5pt] &=-\frac73+3+1\\ &=\frac53 \end{align*}\]
例2
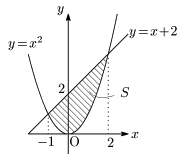
$x^2=x+2$ より,$x^2-x-2=0$.$\therefore x=-1,2$.
\[\begin{align*} S&=\int_{-1}^2\{(x+2)-x^2\}dx\\[5pt] &=-\int_{-1}^2(x^2-x-2)dx\\[5pt] &=-\int_{-1}^2(x+1)(x-2)dx\\[5pt] &=-\left\{-\frac16(2+1)^3\right\}\\[5pt] &=\frac92 \end{align*}\]
例3
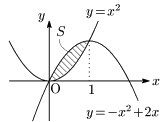
$x^2=-x^2+2x$ より,$x(x-1)=0$.$\therefore x=0,1$.
\[\begin{align*} S&=\int_0^1\{(-x^2+2x)-x^2\}dx\\[5pt] &=-2\int_0^1 x(x-1)dx\\[5pt] &=-2\left\{-\frac16(1-0)^3\right\}\\[5pt] &=\frac13 \end{align*}\]
例4
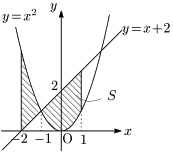
\[S=\int_{-2}^{-1}\{x^2-(x+2)\}dx+\int_{-1}^1\{(x+2)-x^2\}dx\]
ここで,偶関数と奇関数の定積分の公式を用いると,
\[\int_{-1}^1\{(x+2)-x^2\}dx=2\int_0^1(-x^2+2x)dx\]
となるから,
\[\begin{align*} S&=\left[\frac{x^3}3-\frac{x^2}2-2x\right]_{-2}^{-1}-2\left[\frac{x^3}3-2x\right]_0^1\\[5pt] &=\left(\frac73+\frac32-2\right)-2\left(\frac13-2\right)\\[5pt] &=\frac{31}6 \end{align*}\]

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第6章 微分法・積分法
| スライド | ノート | 問題 | |
| 1. 微分係数 | [無料] | ||
| 2. 導関数 | [無料] | ||
| 3. 接線 | [会員] | [会員] | |
| 4. 関数の値の変化 | [会員] | ||
| 5. 極大・極小 | [会員] | ||
| 6. 関数のグラフと方程式・不等式 | [会員] |
| 7. 不定積分 | [無料] | ||
| 8. 定積分 | [会員] | ||
| 9. 様々な定積分 | [会員] | ||
| 10. 面積 | [会員] |