6. 関数のグラフと方程式・不等式(ノート)
基礎をスライドで学ぶ

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]
4. 関数の値の変化	[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]

6.　関数のグラフと方程式・不等式

6.1　グラフと方程式の関係

復習

$\left\{\begin{array}{ll} y=x^2-3x+2&(\mbox{放物線})\\[5pt] y=0&(x\,\mbox{軸}) \end{array}\right.\ \cdots$ ①

の共有点の $x$ 座標は

$x^2-3x+2=0$　(2次方程式) $\cdots$ ②

の実数解．

　逆に，方程式②の実数解は，①の2つのグラフの共有点の $x$ 座標．

補足

　②の実数解は，①以外にもいろいろある．例えば， \[\begin{align*} &\left\{\begin{array}{l} y=x^2-3x\\[5pt] y=-2 \end{array}\right.\\[5pt] &\left\{\begin{array}{l} y=x^2-2x+3\\[5pt] y=x+1 \end{array}\right. \end{align*}\] など．

6.2　関数のグラフと方程式

例題　$x^3-3x^2+1=0$ の解を調べよ．(「求めよ」は難しい．)

　与式の左辺を $f(x)$ とおくと， \[f'(x)=3x^2-6x=3x(x-2)\]

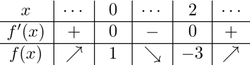
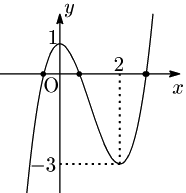
　グラフより，負の解1個と正の解2個をもつ．

補足1

　例えば次のようなグラフでも増減表は上と同じ．

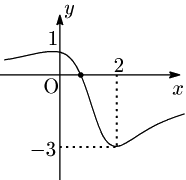
　そこで，「$f(-1)=-3<0$，$f(3)=1>0$」などと書き足せば完璧．（だが3次関数ではやり過ぎ．）

補足2

　増減表からではなく，単調な区間を用いて， \[f(-1)\!=\!-3,f(0)\!=\!1,f(2)\!=\!-3,f(3)\!=\!1\] により， \[-1\!<\!x\!<\!0,\ 0\!<\!x\!<\!2,\ 2\!<\!x\!<\!3\] の範囲にそれぞれ1個ずつ解をもつ，としてもよい．(詳しくは数学Ⅲの中間値の定理を参照)

補足3

　グラフからわかるように，3次方程式では

異なる3個の実数解をもつ
$\iff$ (極大値)×(極小値)$<0$

6.3　関数のグラフと不等式

・$f(x)\geqq0$ を示す
　　→　($f(x)$ の最小値) $\geqq0$ を示す．
・$f(x)\geqq g(x)$ を示す
　　→　$F(x)=f(x)-g(x)$ とおいて，
　　　　　　($F(x)$ の最小値) $\geqq0$
　　　　を示す．

例題　$x\!\geqq\!1$ のとき，不等式 $(x\!+\!1)^3\!\geqq\! 4x^2\!+\!4$ を示せ．

　$f(x)=(x+1)^3-(4x^2+4)$ $(x\geqq1)$ とおくと， \[\begin{align*} f(x)&=x^3-x^2+3x-3\\[5pt] \therefore f'(x)&=3x^2-2x+3\\[5pt] &=3\left(x-\frac13\right)^2+\frac83\\[5pt] &>0 \end{align*}\] 　よって $f(x)$ は $x\geqq1$ で単調に増加するから， \[f(x)\geqq f(1)=0\] 　故に，$x\geqq 1$ で $(x+1)^3\geqq 4x^2+4$

■

---

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]
4. 関数の値の変化	[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]