高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | ||
| 4. 三角関数の導関数 | |||
| 5. 対数関数・指数関数の導関数 | |||
| 6. 媒介変数表示と導関数 | |||
| 7. 陰関数の導関数 | |||
| 8. 平均値の定理 | |||
| 9. 関数の値の変化 | |||
| 10. 関数の極大・極小 | |||
| 11. 関数のグラフ |

10.関数の極大・極小
10.1 極大・極小
極大・極小については数学Ⅱ で既出である.極大や極小については数学Ⅱの方で詳細に説明したのでそちらを参照されたい.
極大値・極小値の定義
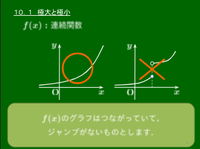
関数 $f(x)$ は連続とする.
$x=a$ を含む開区間で,どんな $x\,(\neq a)$ についても
$f(a)>f(x)$ のとき,$f(a)$ を $f(x)$ の極大値
$f(a)<f(x)$ のとき,$f(a)$ を $f(x)$ の極小値
という.また,極大値と極小値をあわせて極値という.
注意
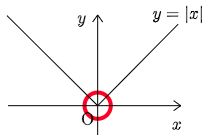
極大・極小は,微分可能性とは無関係である.例えば,関数$f(x)=|x|$ は,$x=0$ で微分可能ではないが,$x=0$ で極小となっている.

10.2 $f(a)$ が極値であるための必要条件
微分可能な関数 $f(x)$ が $x=a$ で極値をとるとする.このとき $f'(a)=0$ が成り立つ.これは数学Ⅱの微分法のときにもお世話になっていたものである.$f'(a)=0$ は $f(x)$ が $x=a$ で極値をとるための必要条件である.
定理 $f(x)$ が微分可能であるとき,
$f(a)$ が極値 $\Longrightarrow\ f'(a)=0$
発展的補足
$f(x)$ が整式の場合などほとんど明らかと思われるこの定理.実際教科書にも証明が書かれていない.しかし例えば次の関数は $x=0$ で極小となるが,$x=0$ の付近で無限回振動するから,本当に $f'(0)=0$ なのかは明らかではない.(この関数については次節10.3に詳細な説明有.)
\[f(x)=\left\{\begin{array}{ll} x^2\left(\cos\dfrac1x+2\right)&(x\neq0)\\[5pt] 0&(x=0) \end{array}\right.\]
そこでこの定理を証明する.
証明
ある開区間で微分可能な関数 $f(x)$ が,区間内の $x=a$ で極大になるとすれば,区間内の任意の $x$ について
$f(x)\leqq f(a)\ \cdots$ ①
が成り立つ.$x=a$ で微分可能であるから
\[\lim_{x\to a}\frac{f(x)-f(a)}{x-a}=f'(a)\]
となるが,①より左辺の分子は常に0以下であることに注意する.ここで $x\to a+0$ のとき,$x-a\to +0$ であるから
\[\lim_{x\to a+0}\frac{f(x)-f(a)}{x-a}\leqq 0\ \ \ \therefore f'(a)\leqq0\]
一方,$x\to a-0$ のとき,$x-a\to -0$ であるから
\[\lim_{x\to a-0}\frac{f(x)-f(a)}{x-a}\geqq 0\ \ \ \therefore f'(a)\geqq0\]
従って,$f'(a)\leqq0$ かつ $f'(a)\geqq0$ となるから, $f'(a)=0$.
$x=a$ で極小となる場合も同様である.
■
注意
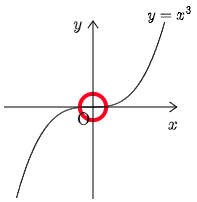
逆 $(\Leftarrow)$ は成り立たない.
(反例) $f(x)=x^3$ のとき,$f'(x)=3x^2$ より $f'(0)=0$.しかるに $f(0)$ は極値ではない.