高校数学[総目次]
高校数学ワンポイント

12. 放物線と2接線で囲まれた部分の面積
1.よくある例題
次は教科書によくある例題と答えです.
例題 $y=x^2$ 上の2点 $(-1,1)$,$(3,9)$ における2本の接線とこの放物線で囲まれた部分の面積 $S$ を求めよ.
解答例
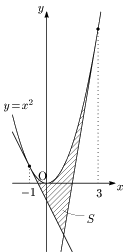
$y’=2x$ より,題意の2本の接線の方程式は
\[\begin{align*}
&y-1=-2(x+1),\\[5pt]
&y-9=6(x-3).
\end{align*}\]
です.整理して
\[y=-2x-1,\ y=6x-9.\]
2接線の交点の $x$ 座標は,$y$ を消去した方程式
\[-2x-1=6x-9\]
を解いて,$x=1$ となります.
従って求める面積 $S$ はグラフの上下関係を考えて,
\[\begin{align*} S&=\int_{-1}^1\!\!\{x^2-(-2x-1)\}dx+\int_1^3\!\!\{x^2-(6x-9)\}dx\\[5pt] &=\int_{-1}^1\!\!(x+1)^2dx+\int_1^3\!\!(x-3)^2dx\\[5pt] &=\left[\frac{(x+1)^3}3\right]_{-1}^1+\left[\frac{(x-3)^3}3\right]_1^3\\[5pt] &=\frac83+\frac83\\[5pt] &=\boldsymbol{\frac{16}3} \end{align*}\]
となります.
※ 最後の定積分を計算するところで,数学Ⅲで出てくる こちら の公式を使いましたが,数学Ⅲを学ばない文系の人たちにもぜひ使えるようになってほしい公式です.
今得られた結果と計算過程から次の3つのことがわかります.
① 2接線の交点の $\boldsymbol{x}$ 座標は,2接点の $\boldsymbol{x}$ 座標の平均である:
\[\frac{-1+3}2=1\]
② 直線 $\boldsymbol{x=1}$ で分けた左右の面積はともに等しく$\boldsymbol{\dfrac83}$ である.
更に,2つの接点を通る直線の方程式を $y=l(x)$ とすると,この直線と放物線で囲まれた部分の面積 $T$ が
\[\begin{align*}
T&=\int_{-1}^3\!\{l(x)-x^2\}dx\\[5pt]
&=-\int_{-1}^3(x+1)(x-3)dx\\[5pt]
&=-\left\{-\frac{(3+1)^3}6\right\}\\[5pt]
&=\frac{32}3
\end{align*}\]
となりますから,先ほど求めた面積を $S$ とすると,
\[S:T=\frac{16}3:\frac{32}3\]
即ち
③ $\boldsymbol{ S:T=1:2}$ である.
ということがいえます.

2.一般論
実は先ほど見た結果は,任意の放物線と,任意の2接線について,いつでも成り立つことなのです.
一般に,次が成り立ちます:
