17．同じものを含む円順列の考え方

高校数学[総目次]

高校数学ワンポイント

	スライド	ノート
1. ファクシミリの原理	[会員]
2. バウムクーヘン分割	[会員]
3. 円と放物線
4. 垂線の長さ
5. 不定方程式
6. 関数の連続性は導関数に遺伝するか
7. 極方程式における $r$ の正負について
8. 極座標表示における扇形分割積分
9. 素因数分解の一意性
10. 三角関数の不定積分
11. コーシー・シュワルツの不等式
12. 放物線と2接線で囲まれた部分の面積
13. 整式の除法(発展編)
14. 3次関数のグラフの特徴
15. 曲線の長さを求める公式の証明について
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法
17. 同じものを含む円順列の考え方
18. $f(f(x))=x$ の形をした関数方程式の取り扱い方
19. パラメータが2次で表された直線の通過領域

17.1 教科書による円順列の説明

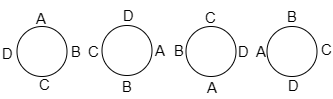
例題　A，B，C，Dの4人が円形に並ぶ方法は何通りあるか．ただし，回転して同じになるものは区別しない．

　少し程度の高い教科書を見ると，円順列に対する考え方が2つ挙げられています。

その1　同じ並び方になる個数に着目する

　この4人を1列に並べる方法は 4！＝24通りです．これらを輪の形にすると区別できないものが4通りずつありますから，$\dfrac{4!}4=3!=6$ (通り)です．詳しくは次節「17.2 「その1」の考え方について，より深く」をご覧ください．

その2　1つを基準にして考える

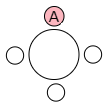
「その1」の考え方では，同じものかどうかを回転させてチェックしなければならず大変です。そこで回転させなくてもいい様に，誰か1人を基準にして，その基準にした1人を固定して考えると，もう回転させてチェックしなくてもよくなります．例えばAを固定して考えると，残りの3人の順列を考えればよくなりますから，

$(4-1)!=3!=6$(通り)

となります．（数学A第1章 場合の数 4.円順列・重複順列 ）

　この2つの方法を比較すると，くるくる回して考えなければならない「その1」よりは，基準を設定して(1つを固定して)考えた「その2」の方が良さそうに見えます．

　ところが同じものを含むような場合では，必ずしも基準を設定する「その2」が適しているという訳でもありません．次の入試問題を見てください．

　この問題の難しさは

基準となるものを設定しづらい

というところにあります．同じものを含んでいる場合であっても，その中にただ1つしかないものも含まれていれば話はずっとシンプルで，例えばこの問題でも赤6白6に加えて黄1というように，1個しかないものがあれば，その黄色を固定して考えればよく，「その2」でも何とかなります．ところがこの問題のようにそういうものがない，すなわちどれも複数個存在している場合には，「その2」でやろうとすると基準が選びにくく，場合分けが多くなりがちです．そこで大活躍するのが「その1」の考え方です．この考え方を用いれば，劇的に負担を軽減できます．

17.2 「その1」の考え方について，より深く

　上の難問題は，先に挙げた「その1」「その2」のどちらの方法でも解くことは可能です．しかし，「その1」つまり「同じ並び方になる個数に着目する」方法は，「その2」つまり「1つを基準にして考える」方法と比べて比較にならないほど容易に答えまでたどり着くことができます．その解法を示す前に，この問題を攻略するための基本姿勢を学んでおきましょう．

異なる4つのものを円形に並べる

　「その1」の考え方，つまり同じ並び方になる個数について，深く掘り下げておきましょう．

　この考え方の基本は「1列に並べた状態で考える」です．

例1 A，B，C，Dの4つの文字を円形に並べる方法は何通りか．

　「ABCD」という並び方を例にとりましょう．この列の左端を右端にもっていくことを4度繰り返すと元のABCDの列に戻ります．これを「周期4の列」と名付けておきます．つまり「周期 $\boldsymbol n$ の列」というのは，左端のものを右端に移動させるという操作を $n$ 回 繰り返すと，元と同じになる列のことです．

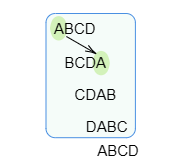
　上の図では列を斜めにずらしながら書いていますが，これは単に見やすさのためにそうしているだけです．そして円順列では青色で囲まれた4つの列は区別しません．他の列でも考えてみましょう．例えばDCBAという列では

\[\rm{DCBA \to CBAD \to BADC \to ADCB \to DCBA}\]

というように周期4の列です．つまり，A，B，C，Dを1列に並べてできる列は，周期4の列となっているため，円順列の方で考えると4重にカウントされてしまっていることになります．従ってA，B，C，Dの4つを円形に並べる方法は，1列に並べたときの順列である $4!$ を，周期4で割って，$\dfrac{4!}4=6$ (通り)となります．

同じものを含むものを円形に並べる

　同じものを含んだこの場合こそが，本稿でお伝えしたい主題です．

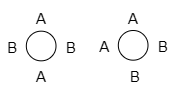
例2 A，A，B，Bの4つを円形に並べる方法は何通りか．

　この4つの文字を1列に並べる方法は，同じものを含む順列の考え方を用いて $\dfrac{4!}{2!2!}=6$ 通りあります．このうちの1つ「ABAB」を例にとりましょう．4文字ですから当然周期4の列です．ところが，この列は次のように周期2の列でもあります．

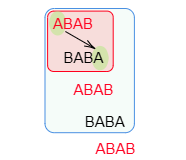
　このように周期 $n$ の列は，周期 $2n$ の列でもあり，周期 $3n$ の列でもありますから，今後周期 $\boldsymbol n$ の列というときには，周期のうちで最も小さいものを指すことにしましょう．数学Ⅱで三角関数を学んだ方は，sin や cos の周期と同じ考え方です．

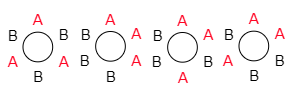
　A，A，B，Bの4つ文字を用いたとき，周期2の列はいくつできるでしょうか？それは「ABAB」と「BABA」の2つだけです．そして残りの $6-2=4$ 通りが周期4の列です．周期2の2つの列は，円順列においては区別されませんから $\dfrac22=1$ 通りとカウントされます．残り4つの周期4の列 AABB，ABBA，BAAB，BBAAは，円順列で考えるとどれも同じで区別されません．つまり1列にして数えた4通りというのは，円順列基準で4重にカウントしていることになります．従って，$\dfrac44=1$ 通りです．

　以上により答えは，周期2の列から1通りと，周期4の列から1通りの合計2通りとなります．

例3 A，A，A，B，B，B の6つを円形に並べる方法は何通りか．

　それでは文字をもう1つずつ増やして，A，A，A，B，B，Bの6つを円形に並べる場合を考えましょう．この6つの文字を1列に並べる方法は，同じものを含む順列の考え方を用いて $\dfrac{6!}{3!3!}=20$ 通りあります．この20通りを周期で分類してみると，周期2の列が「ABABAB」と「BABABA」の2通りで，残りの20－2=18通りが周期6の列です．

注意　A，A，A，B，B，B の6文字から周期3や周期4といった列を作ることはできません．例えば周期3の列を作ろうとすると，この6文字を，3文字ずつ同じ文字から構成される2つのグループに分けなければなりませんが，そのような分け方はできません．

　周期2の列の2通りは，円順列では区別がつきません．ところが1列に並べたときにはこの2通りを区別していますから，円順列で考える際には2重にカウントされていることになります．よって $\dfrac22=1$ 通りです．

　周期6の列の18通りは，円順列で考えると区別のつかないものが6つずつ含まれている，即ち6重にカウントされていますから，円順列では $\dfrac{18}6=3$ 通りになります．

　以上により答えは，周期2の列から1通りと，周期6の列から3通りの合計4通りとなります．

17.3 難問題の解答

　それではいよいよ冒頭の難問題を解決していきましょう．問題を再掲します．

こたえ