高校数学[総目次]

高校数学ワンポイント

  スライド ノート
1. ファクシミリの原理    
2. バウムクーヘン分割    
3. 円と放物線    
4. 垂線の長さ    
5. 不定方程式    
6. 関数の連続性は導関数に遺伝するか    
7. 極方程式における $r$ の正負について    
8. 極座標表示における扇形分割積分    
9. 素因数分解の一意性    
10. 三角関数の不定積分    
11. コーシー・シュワルツの不等式    
12. 放物線と2接線で囲まれた部分の面積    
13. 整式の除法(発展編)    
14. 3次関数のグラフの特徴    
15. 曲線の長さを求める公式の証明について    
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法    
17. 同じものを含む円順列の考え方    
18. $f(f(x))=x$ の形をした関数方程式の取り扱い方    
19. パラメータが2次で表された直線の通過領域    
20. 四面体の面上及び内部を表すベクトル    

20.1 四面体の面上及び内部を表すベクトル

　空間内にある四面体ABCDの面上及び内部にある点Pが，ベクトルを用いてどのように表されるのかを見るのがここでの目標です．結論から先に述べると次のようになります．

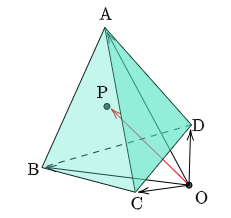
定理　四面体ABCDにおいて，次で表される点Pは，四面体ABCDの面上及び内部に存在する．\[\overrightarrow{\rm OP}=p\,\overrightarrow{\rm OA}+q\,\overrightarrow{\rm OB}+r\,\overrightarrow{\rm OC}+s\,\overrightarrow{\rm OD}\]\[p+q+r+s=1,\ p\geqq0,\ q\geqq0,\ r\geqq0,\ s\geqq0\]

　いきなりこれを証明するのは難しいので，まずは三角形の周及び内部を表すベクトルの復習から始めていきましょう．その場合の事実が，空間内の四面体のケースにそのまま使えるのです．

20.2 三角形の周及び内部を表すベクトル

まずは三角形の周及び内部を表すベクトルの復習から

　平面ベクトルの応用 のところで，三角形の周及び内部を表すベクトルを学習しました．

三角形の周及び内部　△ABCに対して，点Pが\[\overrightarrow{\mathstrut\rm AP}=r\overrightarrow{\mathstrut\rm AB}+s\overrightarrow{\mathstrut\rm AC},\ r+s\leqq1,\ r\geqq 0,\ s\geqq 0\]を満たしながら動くとき，Pは△ABCの周及び内部にある．

※これが何故いえるのかはこちら をご覧ください．

　$\overrightarrow{\mathstrut\rm AB}$ と $\overrightarrow{\mathstrut\rm AC}$ の係数にはしばしば $s$ と $t$ が用いられますが，冒頭の定理の四面体のケースに接続させるために $r$ と $s$ にしています．いま，この式の始点をすべて点Oに書き換えると

\[\overrightarrow{\rm OP}-\overrightarrow{\rm OA}=r(\overrightarrow{\rm OB}-\overrightarrow{\rm OA})+s(\overrightarrow{\rm OC}-\overrightarrow{\rm OA})\]

\[\therefore \overrightarrow{\rm OP}=(1-r-s)\overrightarrow{\rm OA}+r\overrightarrow{\rm OB}+s\overrightarrow{\rm OC}\]

となります．$1-r-s=q$ とおくと，係数の条件は

$q+r+s=1,\ r+s\leqq1,\ r\geqq0,\ s\geqq0\ \cdots$ ①

となりますが，$q=1-(r+s)$ ですから，$r+s\leqq1$ であることと $q\geqq0$ であることは同値です．従って

① $\iff q+r+s=1,\ q\geqq0,\ r\geqq0,\ s\geqq0$

となりますから次が成り立ちます．

三角形の周及び内部(その2)　△ABCに対して，点Pが\[\overrightarrow{\rm OP}=q\,\overrightarrow{\rm OA}+r\,\overrightarrow{\rm OB}+s\,\overrightarrow{\rm OC}\]\[q+r+s=1,\ q\geqq0,\ r\geqq0,\ s\geqq0\]を満たしながら動くとき，Pは△ABCの周及び内部にある．

　ここで重要な注意をしておきます。証明の最初のところで，始点をOに書き換えましたが，点Oとしてはあらゆる点が許されます．文字がOだと何となく座標平面の原点という印象を伴いがちですが，それならQやRにでもしておけばよいのです．それだけではありません．この点Oは平面ABC上に乗っている必要すらないのです。つまり，四面体OABCの頂点のように，平面ABCから離れたところから点Oをとってきてもよいのです．

　以上で，定理を証明する準備は完了です．

20.3 冒頭の定理の証明

　前節の最後に導いた「三角形の周及び内部(その2)」を利用して，冒頭の定理を証明していきましょう．定理を再掲しておきます．

定理　四面体ABCDにおいて，次で表される点Pは，四面体ABCDの面上及び内部に存在する．\[\overrightarrow{\rm OP}=p\,\overrightarrow{\rm OA}+q\,\overrightarrow{\rm OB}+r\,\overrightarrow{\rm OC}+s\,\overrightarrow{\rm OD}\]\[p+q+r+s=1,\ p\geqq0,\ q\geqq0,\ r\geqq0,\ s\geqq0\]

証明

　$p+q+r+s=1$ より $p=1-q-r-s$．これを与えられたベクトルの式に代入して