置換積分法(いくつかの重要例題と偶関数・奇関数の定積分)

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート	問題
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質
5. 置換積分法（定積分）
6. 部分積分法（定積分）
7. 定積分と微分法
8. 定積分と和の極限
9. 定積分と不等式
10. 定積分の応用（面積）
11. 定積分の応用（体積）
12. 定積分の応用（回転体の体積）
13. 曲線の長さ

5．置換積分法(定積分)

5.1 定積分の置換積分法

　関数 $f(x)$ は区間 $[a,b]$ で連続，更に $x$ は微分可能な関数 $g(t)$ により $x=g(t)$ で表されているとする．そして，$t$ が $\alpha$ から $\beta$ まで変化したとき，$x$ は $a$ から $b$ まで変化したとする．

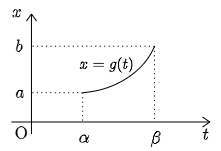
　このとき，$f(x)$ の不定積分を $F(x)$ とすれば，置換積分法の公式(Ⅰ)により，
$$\begin{align*} \int\!f(g(t))g'(t)\,dt&=\int\!f(x)\,dx\\[5pt] &=F(x)+C\\[5pt] &=F(g(t))+C \end{align*}$$
であるから，
$$\begin{align*} \int_\alpha^\beta\!\!f(g(t)g'(t)\,dt&=\Bigl[F(g(t))\Bigr]_\alpha^\beta\!\\[5pt] &=F(g(\beta))-F(g(\alpha))\\[5pt] &=F(b)-F(a)\\[5pt] &=\int_a^b\!\!f(x)dx \end{align*}$$
となる．

定積分の置換積分法 $$\int_a^b\!\!f(x)\,dx=\int_\alpha^\beta\!\!f(g(t))g'(t)\,dt$$

発展的補足

　$x=g(t)$ の選び方についてはあまり神経質になる必要はないが，厳密には次のような点に注意して選ぶ．

• 積分区間で単調な関数を選ぶのが普通．
• 単調でない関数を選ぶ場合は次の3条件を満たせばよい：

  • $a=g(\alpha),\ b=g(\beta)$ で，$t$ が $\alpha\to\beta$ と変化するとき， $x$ は連続的に $a\to b$ と変化する．
  • 閉区間 $[\alpha,\ \beta]$ で $g'(t)$ は連続．
  • 閉区間 $[\alpha,\ \beta]$ で $f(g(t))$ は連続．

重要例題3選

　以下の3つの例題は基本的，かつ重要で，入試問題等にしばしば登場する．

例題1　$a>0$ のとき，$\displaystyle\int_0^a\!\!\sqrt{a^2-x^2}\,dx$ を計算せよ．

答

　解答例を表示する

　$x=a\sin\theta$ とおくと，
$$dx=a\cos\theta\,d\theta,\ \ \begin{array}{c|c} x&0\to a\\\hline \theta&0\to\frac\pi2 \end{array},$$
$$\sqrt{a^2-x^2}=\sqrt{a^2(1-\sin^2\theta)}=a|\cos\theta|$$
であるから，
$$\begin{align*} \int_0^a\!\!\sqrt{a^2-x^2}\,dx&=\int_0^{\frac\pi2}\!\!a|\cos\theta|\cdot a\cos\theta\,d\theta\\[5pt] &=a^2\int_0^{\frac\pi2}\cos^2\theta\,d\theta\\[5pt] &=\frac{a^2}2\int_0^{\frac\pi2}\!\!(1+\cos2\theta)\,d\theta\\[5pt] &=\frac{a^2}2\Bigl[\theta+\frac12\sin2\theta\Bigr]_0^{\frac\pi2}\\[5pt] &=\underline{\frac{\pi a^2}4} \end{align*}$$

例題2　$\displaystyle\int_0^a\!\!\frac1{a^2+x^2}\,dx$ を計算せよ．

答

　解答例を表示する

　$x=a\tan\theta$ とおくと，
$$dx=\frac a{\cos^2\theta}\,d\theta,\ \ \begin{array}{c|c} x&0\to a\\\hline \theta&0\to\frac\pi4 \end{array},$$
$$\frac1{a^2+x^2}=\frac1{a^2(1+\tan^2\theta)}=\frac{\cos^2\theta}{a^2}$$
であるから，
$$\begin{align*} \int_0^a\!\!\frac1{a^2+x^2}\,dx&=\int_0^{\frac\pi4}\frac{\cos^2\theta}{a^2}\cdot\frac a{\cos^2\theta}\,d\theta\\[5pt] &=\frac 1a\int_0^{\frac\pi4}d\theta\\[5pt] &=\underline{\frac\pi{4a}} \end{align*}$$

例題3(重要)　次を示せ． $$\int_0^a\!\!f(x)\,dx=\int_0^a\!\!f(a-x)\,dx$$

答