数学Ⅱ微分法 接線の方程式の求め方｜曲線上の点・外部の点・共通接線までスライドで学ぶ

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート	問題
1. 微分係数
2. 導関数
3. 接線
4. 関数の値の変化
5. 極大・極小
6. 関数のグラフと方程式・不等式

7. 不定積分
8. 定積分
9. 様々な定積分
10. 面積

3.　接線

3.1　接線の方程式

接線とは何か

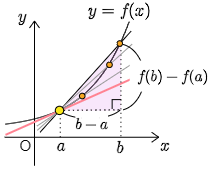
　曲線 $y=f(x)$ 上の点 P$(a,f(a))$ を通り，傾きが $f'(a)$ である直線を，曲線 $y=f(x)$ の点 $(a,f(a))$ における接線という．この接線が上の図のような直線を表していることは，微分係数 $f'(a)$ が曲線 $y=f(x)$ 上の2点を結ぶ線分の傾きの極限値であるということから理解できる．(下図)

　既に2次関数や円のところでも接線は出てきており，そこでは「接線＝共有点がただ1つの直線」という説明がなされていた．2次関数や円といった枠組みの中ではそれでもよかったが，今後は様々な曲線を相手に接線を考えていくことになるため，「微分係数 $f'(a)$ を傾きにもつ直線」と理解しておく方が混乱が少なかろう．もちろんこの定義は2次関数や円でも($y$ 軸に平行な接線など特別なものを除けば)通用する．

　点Pにおける接線は，点P$(a,\ f(a))$ を通る傾き $f'(a)$ の直線であるからその方程式は次のようになる：

接線の方程式　曲線 $y=f(x)$ 上の点 $(a,f(a))$ における接線の方程式は\[y-f(a)=f'(a)(x-a)\]

例題　曲線 $y=x^2$ 上の点 $(1,1)$ における接線の方程式を求めよ．

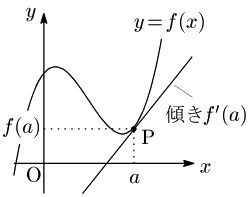
2.2　曲線上にない点から引いた接線

例題　点$(0,2)$から曲線 $y=x^3$ に引いた接線の方程式，及び接点の座標を求めよ．

解法は大きく2つ　何といっても解法1がオススメ

解法1　[接点からスタート]

　$y’=3x^2$ により，曲線上の点 $(t,t^3)$ における接線の方程式は， \[\begin{align*} y-t^3&=3t^2(x-t)\\[5pt] \therefore y&=3t^2x-2t^3 \end{align*}\] 　これが点 $(0,2)$ を通るとき，$2=-2t^3$

　整理して　$t^3+1=0$

　$t$ は実数であるから，$ t=-1$

　よって，
　　接線の方程式：$\underline{\boldsymbol{y=3x+2}}$
　　接点の座標：$\underline{\boldsymbol{(-1,-1)}}$

解法2　[直線からスタート]

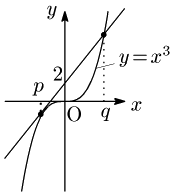
　点 $(0,2)$ を通る直線の方程式は，$y=mx+2$ とおける．
　ここで，接点，及び他の共有点の $x$ 座標をそれぞれ $p, q$ とすると， \[x^3-(mx+2)=(x-p)^2(x-q)\] という恒等式が成り立つ$^*$．

　(注)$^*$　詳しくは次節「発展的補足」参照．

よって右辺を展開して整理し，両辺の係数を比較すると， \[\left\{ \begin{array}{rl} 0=\!\!&-2p-q\\[5pt] -m=\!\!&p^2+2pq\\[5pt] -2=\!\!&-p^2q \end{array} \right.\] 　これを解くと，$p=-1$，$q=2$，$m=3$．
　故に，
　　接線の方程式：$\underline{\boldsymbol{y=3x+2}}$
　　接点の座標：$\underline{\boldsymbol{(-1,-1)}}$

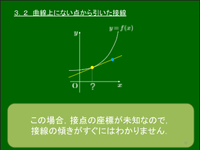
3.3　共通接線

　2曲線に接する直線を，その2曲線の共通接線という．共通接線は大別すると

　　1．接点を共有している
　　2．接点が異なっている

の2タイプがある．

1．接点を共有している場合