高校数学[総目次]
第6章 微分法・積分法
| スライド | ノート | 問題 | |
| 1. 微分係数 | |||
| 2. 導関数 | |||
| 3. 接線 | |||
| 4. 関数の値の変化 | |||
| 5. 極大・極小 | |||
| 6. 関数のグラフと方程式・不等式 |
| 7. 不定積分 | |||
| 8. 定積分 | |||
| 9. 様々な定積分 | |||
| 10. 面積 |

5.極大・極小(数学Ⅱ微分法)
演習問題
問題1【標準】
関数 $f(x)=x^3-3ax$ $ (0\leqq x\leqq1)$ の最大値と最小値を次の各場合について求めよ.ただし,$a$ を定数とする.
(1) $0\leqq a<1$
(2) $a\geqq1$
問題2【標準】
$a$ を定数とする.関数 $f(x)=x^3-3x^2+2$ の $0\leqq x\leqq a$ $(a>0)$ における最大値と最小値を求めよ.
問題3【標準】
関数 $f(x)=ax^3+3ax^2+b$ $(-1\leqq x\leqq 2)$ の最大値が10,最小値が $-8$ であるように,定数 $a,\ b$ の値を定めよ.
問題4【標準】
$a>0$ とする.関数 $f(x)=ax^4-4ax^3+b$ $(1\leqq x\leqq 4)$ の最大値が5,最小値が $-4$ であるように,定数 $a,\ b$ の値を定めよ.
問題5【標準】
放物線の一部 $y=3-x^2,\ y\geqq0$ と $x$ 軸に平行な直線が異なる2点A,Bで交わるとき,原点をOとして,△OABの面積の最大値と,そのときの点A,Bの座標を求めよ.ただし,Aの $x$ 座標は負とする.
問題6【標準】
周囲の長さが $2s$ ($s$ は定数) である二等辺三角形の面積の最大値を求めよ.また,そのときの三角形はどのような形か.
問題7【発展】
$x,\ y$ は $x^2+y^2=2$,$x\geqq0$,$y\geqq0$ を満たしている.$x+y=t$ とおくとき,次の各問いに答えよ.
(1) $t$ の取りうる値の範囲を求めよ.
(2) $x^3+y^3$ を $t$ で表し,そのとりうる値の範囲を求めよ.
問題8【発展】
$0\leqq\theta<2\pi$ とする.与えられたように,変数を $t$ に置き換えて,次の関数の最大値と最小値を求めよ.また,そのときの $\theta$ の値を求めよ.
(1) $y=2\sin^3\theta-3\sin^2\theta$ $\sin\theta=t$
(2) $y=\cos2\theta-2\cos^3\theta$ $\cos\theta=t$
問題9【発展】
$x>1,\ y>1,\ xy=4$ であるとき,$4(\log_2x)^3+(\log_2y)^3$ の値が最小となるような $x,\ y$ の値を求めよ.
問題10【発展】
$a$ を定数とする.関数 $f(x)=\dfrac14x^3+\dfrac34x-2-6x$ の $-a\leqq x\leqq a$ $(a>0)$ における最大値を $m(a)$ とするとき,関数 $y=m(a)$ のグラフをかけ.

解答
$f'(x)=3x^2-3a^2=3(x+a)(x-a)$.
(1) $0\leqq a<1\ (\cdots$ ①) のとき
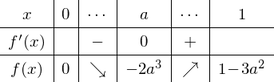
$1^\circ$ ①かつ $1-3a^2>0$ すなわち $0\leqq a<\dfrac{\sqrt3}3$ のとき
$x=1$ で最大値 $1-3a^2$
$x=a$ で最小値 $-2a^3$
$2^\circ$ ①かつ $1-3a^2=0$ すなわち $a=\dfrac{\sqrt3}3$ のとき
$x=0,1$ で最大値 $0$
$x=\dfrac{\sqrt3}3$ で最小値 $-\dfrac{2\sqrt3}9$
$3^\circ$ ①かつ $1-3a^2<0$ すなわち $\dfrac{\sqrt3}3<a<1$ のとき
$x=0$ で最大値 $0$
$x=a$ で最小値 $-2a^3$
(2) $a\geqq1$ のとき
$0\leqq x\leqq1$ の範囲で $f'(x)=3(x^2-a^2)\leqq 3(1^2-1^2)=0$ となるから,この範囲で $f(x)$ は単調に減少する.よって
$x=0$ で最大値 $0$
$x=1$ で最小値 $1-3a^2$
