高校数学[総目次]
数学Ⅲ 第3章 積分法
| スライド | ノート | 問題 | |
| 1. 不定積分 | [無料] | ||
| 2. 置換積分法(不定積分) | [無料] | ||
| 3. 部分積分法(不定積分) | [無料] | ||
| 4. 定積分とその性質 | |||
| 5. 置換積分法(定積分) | |||
| 6. 部分積分法(定積分) | |||
| 7. 定積分と微分法 | |||
| 8. 定積分と和の極限 | |||
| 9. 定積分と不等式 | |||
| 10. 定積分の応用(面積) | |||
| 11. 定積分の応用(体積) | |||
| 12. 定積分の応用(回転体の体積) | |||
| 13. 曲線の長さ |

10.定積分の応用(面積)
10.1 面積
関数 $y=f(x)$ が区間 $[a,\ b]$ で常に0以下の値をとるとする.このとき定積分 $\displaystyle \int_a^b f(x)\,dx$ の値は,$y=f(x)$ のグラフと $x$ 軸,及び2直線 $x=a$,$x=b$ とで囲まれた部分の面積を $S$ とすれば,数学Ⅱの積分法のところで学んだように $-S$ となるのであった.
\[\int_a^b f(x)\,dx=-S\]
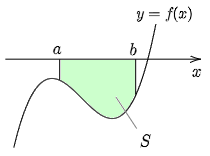
一般には関数 $y=f(x)$ は,区間 $[a,\ b]$ で正の値をとったり負の値をとったりすることがあるため,$x$ 軸,及び2直線 $x=a$,$x=b$ とで囲まれた部分の面積が知りたい場合は,符号が入れ替わるごとに積分区間を分けて計算しなければならない.例えば,$y=f(x)$ のグラフが下の図1のような場合,赤色と青色の面積の合計を $T$ とすると
\[T=\int_a^c f(x)\,dx-\int_c^d f(x)\,dx+\int_d^b f(x)\,dx\]
という具合にして求めることになる.
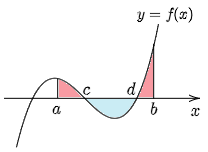
ところでこの面積の合計は,関数全体に絶対値をかぶせた $y=|f(x)|$ を用いれば,次の図2からわかるように,符号を気にすることなく
\[T=\int_a^b|f(x)|\,dx\]
と表現できる.
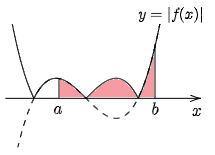
まとめ 閉区間 $[a,\ b]$ で連続な関数 $f(x)$ のグラフと $x$ 軸,及び2直線 $x=a$,$x=b$ とで囲まれる部分の面積は
\[\int_a^b|f(x)\,|dx\]
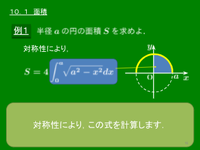
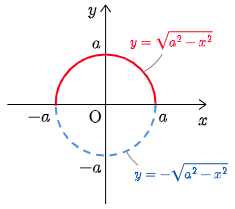
例題1 半径 $a$ の円の面積 $S$ を求めよ.
こたえ

補足
この問題では「半径 $a$ の円の面積を求めよ」であったから,$\displaystyle S=4\int_0^a\sqrt{a^2-x^2}\,dx$ の計算のところで置換積分を行わなければならなかった.入試問題を解いていると,しばしば $\displaystyle\int_\alpha^\beta\!\!\sqrt{a^2-x^2\ }\,dx$ の形の積分計算が必要になるが,そのときには逆に式の意味からこの積分が円の面積(の一部)を表していることに注目して,置換積分を行うのではなく,一気に答えまでもっていくのが実践的である.以下その例をいくつか挙げる.
$a>0$ のとき
① $\displaystyle \int_0^a\sqrt{a^2-x^2}\,dx=\frac{\pi a^2}4$
→ 半径 $a$ の円の面積の $\dfrac14$