高校数学[総目次]
数学Ⅲ 第3章 積分法
| スライド | ノート | 問題 | |
| 1. 不定積分 | [無料] | ||
| 2. 置換積分法（不定積分） | [無料] | ||
| 3. 部分積分法（不定積分） | [無料] | ||
| 4. 定積分とその性質 | [会員] | ||
| 5. 置換積分法（定積分） | [会員] | ||
| 6. 部分積分法（定積分） | [会員] | ||
| 7. 定積分と微分法 | [会員] | ||
| 8. 定積分と和の極限 | [会員] | ||
| 9. 定積分と不等式 | [会員] | ||
| 10. 定積分の応用（面積） | [会員] | ||
| 11. 定積分の応用（体積） | [会員] | [会員] | |
| 12. 定積分の応用（回転体の体積） | [会員] | ||
| 13. 曲線の長さ |
11．定積分の応用(体積)
11.1 体積と積分
定積分で面積を計算してきたが，今度は体積を計算する．
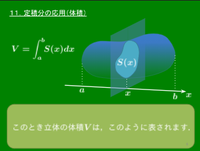
定積分と体積 空間内の立体を平面で切り，この平面と垂直に $x$ 軸をとって切り口の面積を $S(x)$ とすると，この立体の平面 $x=a$ と平面 $x=b$ (ただし $a < b$ ) との間にある部分の体積 $V$ は \[V=\int_a^b\!\!S(x)\,dx\] である．
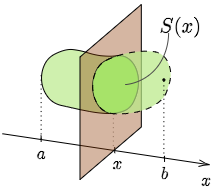
早い話が体積を求めるには断面積がわかればよいということであるが，どういう切り口を考えるかで計算の煩雑さが大きく異なる場合が多い．
また，立体の全体像がイメージできなくても，断面積さえわかれば体積は計算できる．
証明
2平面 $x=a,x=t$ で挟まれる部分の体積を $V(t)$ とすると，\[V=V(b)\]
である．
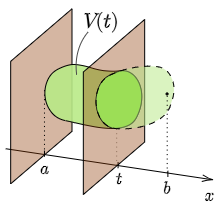
挟まれた部分が $V(t)$
$\Delta t > 0$のとき，$\Delta V=V(t+\Delta t)-V(t)$ とおき，区間 $[t,t+\Delta t]$ における $S(t)$ の最小値を $m$，最大値を $M$ とすると， \[m\Delta t\leqq \Delta V\leqq M\Delta t\] \[\therefore m\leqq\frac{\Delta V}{\Delta t}\leqq M\] ここで，$\Delta t\to +0$ とすると， \[m\to S(t),\ M\to S(t)\] であるから，はさみうちの原理により \[\lim_{\Delta t\to+0}\frac{\Delta V}{\Delta t}=S(t)\ \cdots\mbox{①}\] $\Delta t < 0$ のときも同様にして， \[\lim_{\Delta t\to -0}\frac{\Delta V}{\Delta t}=S(t)\ \cdots\mbox{②}\] ①，②により， \[\lim_{\Delta t\to 0}\frac{\Delta V}{\Delta t}=S(t)\] この式の左辺は， \[\mbox{左辺}=\lim_{\Delta t\to 0}\frac{V(t+\Delta t)-V(t)}{\Delta t}=\frac{dV}{dt}\] であるから結局 \[\frac{dV}{dt}=S(t)\] である．つまり $V(t)$ は $S(t)$ の不定積分であることがわかった．従って， \[V(b)-V(a)=\int_a^b\!\!S(t)\,dt\] $V(t)$ のおき方から $V(a)=0$ であるから， \[V(b)(=V)=\int_a^b\!\!S(t)\,dt\]
■
11.2 例題
体積を求める図形には大きく分けて，回転体と非回転体の2つがある．回転体における断面積は，回転軸に垂直な平面で切った切り口を考えればよいというパターンがあるのに対して，非回転体では一定のパターンがない．どの断面積を考えれば計算が簡単になるかというセンスが問われるものも多く，一般には難問化しやすい．以下では非回転体の代表的な問題を取り上げる．
(回転体の体積については次節の第12節で詳細に述べる．)
例題 直円柱 $x^2+y^2\leqq1,\ 0\leqq z\leqq1$ を平面 $y=z$ で切ったとき，小さい方の体積$V$を求めよ．
その1 [ $x$ 軸に垂直な平面で切る]
$x$ 軸に垂直な平面で切った切り口は直角二等辺三角形で，その面積は \[\frac12\Bigl(\sqrt{1-x^2}\Bigr)^2=\frac12(1-x^2)\] であるから， \[\begin{align*} V&=\int_{-1}^1\!\!\frac12(1-x^2)\,dx\\ &=-\frac12\int_{-1}^1\!\!(x+1)(x-1)\,dx\\ &=-\frac12\cdot\left\{-\frac{(1+1)^3}6\right\}\\ &=\underline{\frac23} \end{align*}\]
その2 [ $y$ 軸に垂直な平面で切る]
$y$ 軸に垂直な平面で切った切り口は長方形で，その面積は \[y\times2\sqrt{1-y^2}\] であるから， \[\begin{align*} V&=2\int_0^1\!\!y\sqrt{1-y^2}\,dy\\ &=2\left[-\frac13(1-y^2)^{\frac32}\right]_0^1\\ &=\underline{\frac23} \end{align*}\]
このページで疑問は解決されましたか？
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第3章 積分法
| スライド | ノート | 問題 | |
| 1. 不定積分 | [無料] | ||
| 2. 置換積分法（不定積分） | [無料] | ||
| 3. 部分積分法（不定積分） | [無料] | ||
| 4. 定積分とその性質 | [会員] | ||
| 5. 置換積分法（定積分） | [会員] | ||
| 6. 部分積分法（定積分） | [会員] | ||
| 7. 定積分と微分法 | [会員] | ||
| 8. 定積分と和の極限 | [会員] | ||
| 9. 定積分と不等式 | [会員] | ||
| 10. 定積分の応用（面積） | [会員] | ||
| 11. 定積分の応用（体積） | [会員] | [会員] | |
| 12. 定積分の応用（回転体の体積） | [会員] | ||
| 13. 曲線の長さ |